对于循环神经网络，它的输入是一段不定长的序列，输出却是定长的。然而，很多问题的输出也是不定长的序列，比如机器翻译。当输入输出都是不定长序列时，我们可以使用编码器-解码器 (encoder-decoder) 来对其进行建模。

介绍 Introduction

在很多 NLP 应用中，输入和输出都可以是不定长序列。以机器翻译为例，输入可以是一段不定长的中文文本序列，输出可以是一段不定长的英语文本序列，例如

中文输入：”知”, “识”, “就”, “是”, “力”, “量”

英语输出：”Knowledge”, “is”, “power”

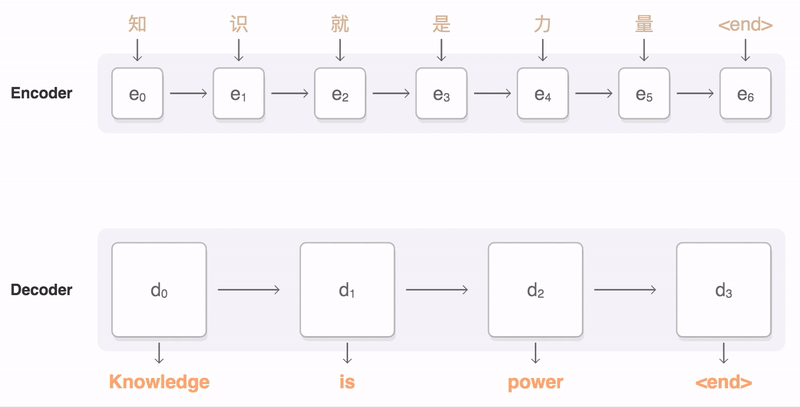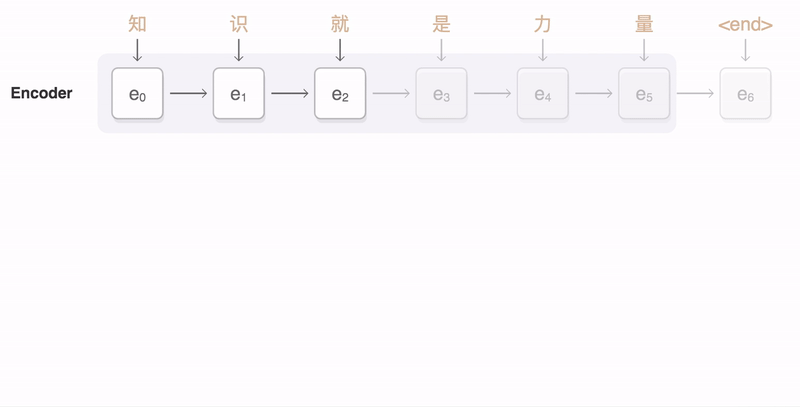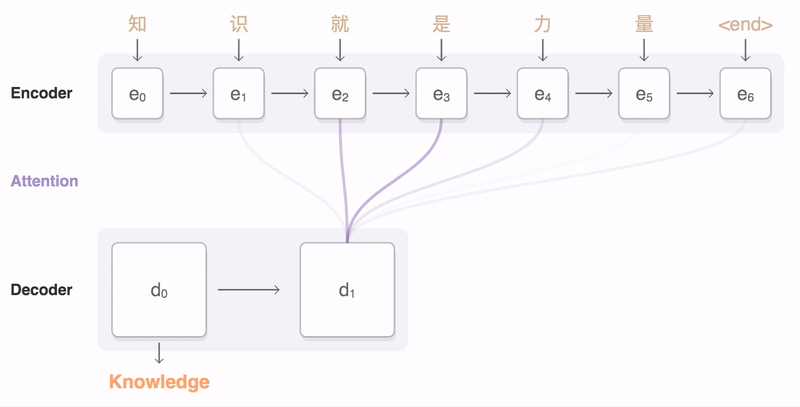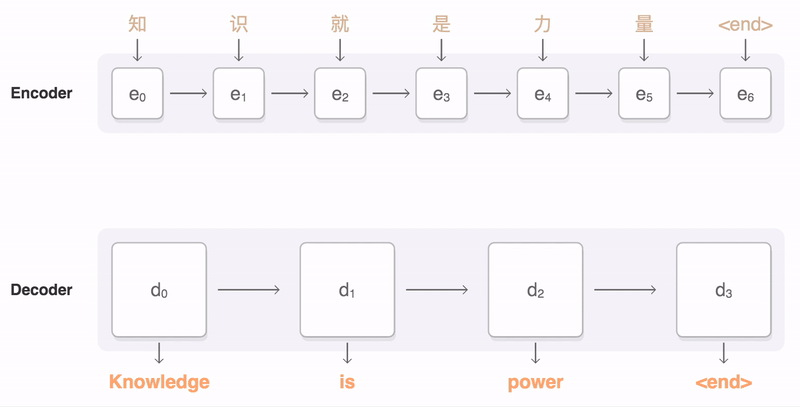
当输入输出都是不定长序列时，我们可以使用编码器-解码器 (encoder-decoder) 或者 seq2seq。它们分别基于2014年的两个工作：

Cho et al., Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation
Sutskever et al., Sequence to Sequence Learning with Neural Networks

Cho 是 Yoshua Bengio 团队的，论文中 RNN Cell 使用的是 GRU，这也是 GRU 首次被提出！Sutskever 是谷歌团队的，论文中 RNN Cell 用的是 LSTM。RNN Cell 的不同是这两篇论文的主要区别。

这两个工作几乎是同时提出，本质上都用到了2个循环神经网络 (RNN)，分别叫做编码器 (Encoder) 和解码器 (Decoder)。编码器对应于输入序列，将输入序列的信息编码到上下文变量 (context variable) 中；解码器对应输出序列，将上下文变量解码成输出序列。

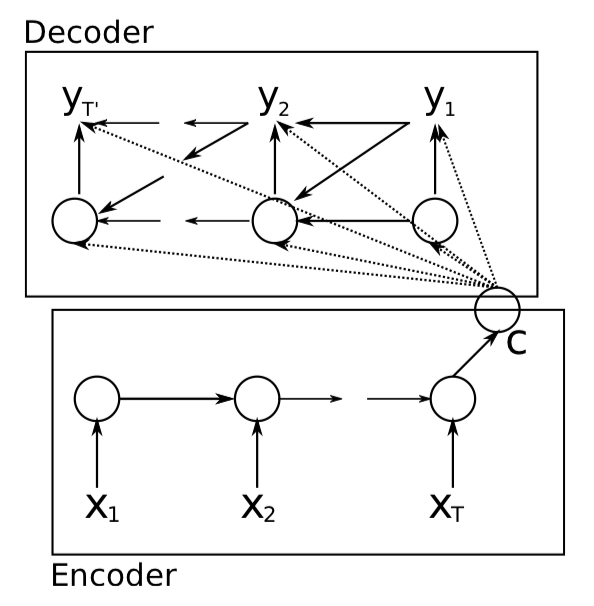
在普通的编码器-解码器模型中，有一个很大的局限性。那就是上下文变量对于 Decoding 阶段每个时间步都是一样的，这可能是模型性能的一个瓶颈。我们希望不同时间步的解码能够依赖于与之更相关的上下文信息，换句话说，Decoding 往往并不需要整个输入序列的信息，而是要有所侧重。于是，Bengio 团队的 Bahdanau 在 2014年首次在编码器-解码器模型中引入了注意力机制 (Attention Mechanism)：

Bahdanau et al., Neural Machine Translation by Jointly Learning to Align and Translate

在介绍编码器-解码器的设计之前，先简单介绍一下循环神经网络 (下文中用 RNN 指代)。

循环神经网络 RNN

循环神经网络 (Recurrent Neural Network) 是一类用于处理序列数据的神经网络。它不是刚性地记住所有固定长度的序列，而是通过隐藏状态来储存前面时间的信息。在 RNN 中，当前时刻的隐层节点的输出会作为下一时刻的隐层节点的输入，使得她可以保留之前的信息。

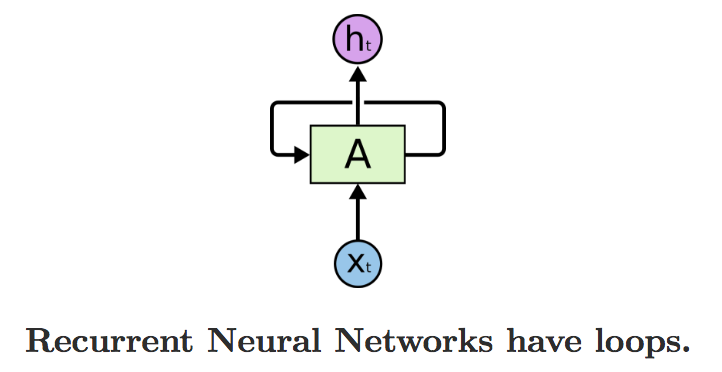
这个循环的结构让 RNN 看起来有些难以理解。但是，RNN 其实与普通的神经网络有不少相似之处。我们可以按时间维度将其展开，如下图所示：

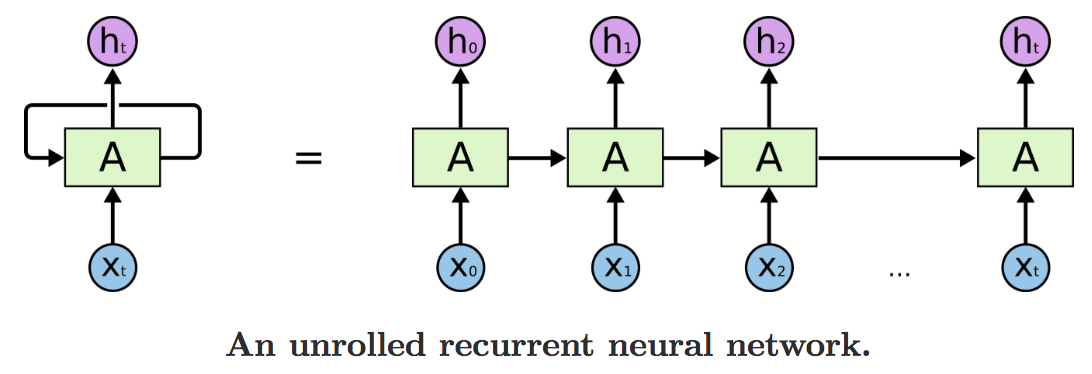
RNN 的链状结构让她看起来就像是为序列数据而生。

原始的 BP 神经网络 (或者原始 CNN) 最大的局限之处在于：它们将固定大小的向量作为输入 (比如一张图片)，然后输出一个固定大小的向量 (比如不同分类的概率)。而且：这些模型按照固定的计算步骤来 (比如模型中 layer 的数量) 实现这样的映射。RNN 的特别之处在于，她允许我们控制向量序列的长度：输入序列、输出序列、或者输入输出序列。通过下面几个例子可以具体理解这点：

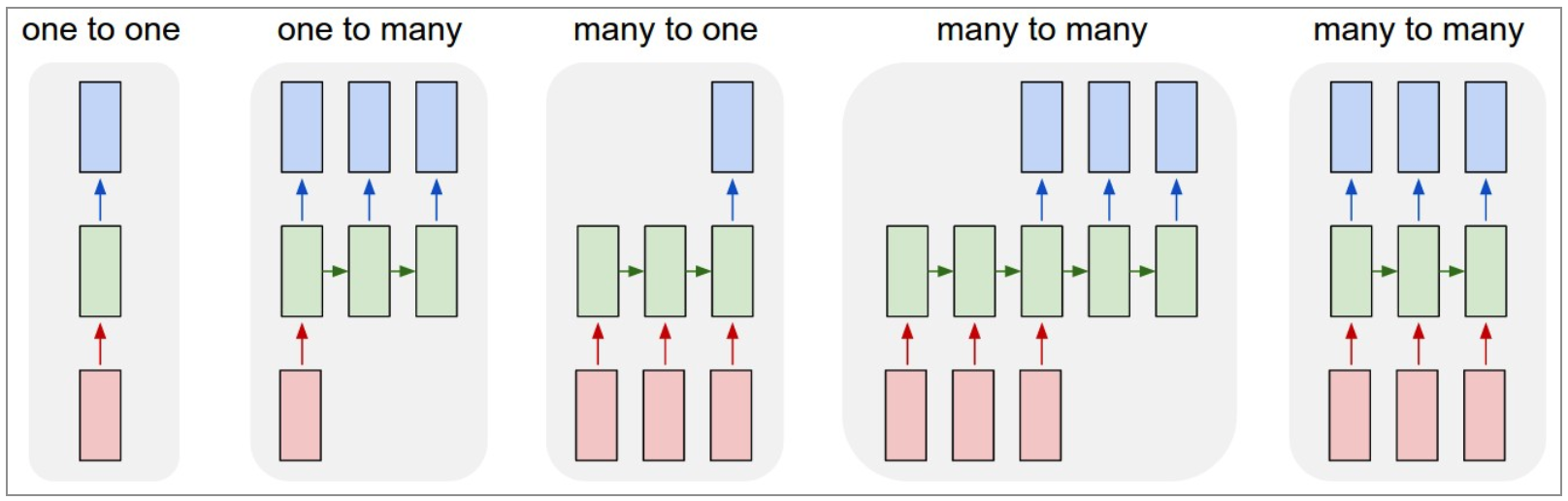
每一个矩形是一个向量，箭头则表示函数 (比如矩阵乘法)。输入向量用红色标出，输出向量用蓝色标出，绿色的矩形是 RNN 的状态。从左到右：

1->1: 没有使用 RNN 的原始模型，从固定大小的输入得到固定大小输出 (比如图像分类)
1->N: 序列输出 (比如图片字幕，输入一张图片输出一段文字序列)
N->1: 序列输入 (比如情感分析，输入一段文字然后将它分类成积极或者消极情感)
N->M: 序列输入和序列输出 (比如机器翻译：一个 RNN 读取一条中文语句然后将它以英语形式输出)
N->N: 同步序列输入输出 (比如视频分类，对视频中每一帧打标签)。

我们注意到在每一个案例中，都没有对序列长度进行预先特定约束，因为递归变换 (绿色部分) 是固定的，而且我们可以根据需要多次使用。

在近些年，人们利用 RNN 不可思议地解决了各种各样的问题：语音识别，语言模型，翻译，图像描述，等等。关于 RNN 在这些方面取得的惊人成功，我们可以看 Andrej Karpathy 的博文：The Unreasonable Effectiveness of Recurrent Neural Networks.

RNN 之所以能够取得这样的成功，主要是因为 LSTM / GRU 的使用。他们都是带门控 (gate) 的 RNN 单元，用于解决长期依赖 (long-term dependencies) 的问题，对于很多任务，比普通的 RNN 单元效果要好很多！基本上现在所使用的循环神经网络用的都是 LSTM / GRU 单元。

介绍完了 RNN，让我们回到这篇文章的主题，编码器-解码器。编码器和解码器都是 RNN，上下文变量为二者搭建起了信息传递的桥梁，编码器将输入序列的信息编码到上下文变量中，解码器将上下文变量中的信息解码生成输出序列。编码器-解码器的设计是多种多样的，需要根据具体问题具体分析。

编码器-解码器 Encoder-Decoder

在很多应用中，输入和输出都可以是不定长序列。以机器翻译为例，输入可以是一段不定长的英语文本序列，输出可以是一段不定长的法语文本序列，例如

英语输入：“They”、“are”、“watching”、“.”

法语输出：“Ils”、“regardent”、“.”

当输入输出都是不定长序列时，我们可以使用编码器—解码器 (encoder-decoder) 或者 seq2seq 模型。这两个模型本质上都用到了两个循环神经网络，分别叫做编码器和解码器。编码器对应输入序列，解码器对应输出序列。

下图描述了使用编码器—解码器将上述英语句子翻译成法语句子的一种方法。在训练数据集中，我们可以在每个句子后附上特殊符号 “<eos>” (end of sequence) 表示序列的终止。编码器每个时间步的输入依次为英语句子中的单词、标点和特殊符号 “<eos>”。下图使用了编码器在最终时间步的隐藏状态作为输入句子的编码信息。解码器在各个时间步中使用输入句子的编码信息和上个时间步的输出以及隐藏状态作为输入。

我们希望解码器在各个时间步能正确依次输出翻译后的法语单词、标点和特殊符号 “<eos>”。
需要注意的是，解码器在最初时间步的输入用到了一个表示序列开始的特殊符号 “<bos>” (beginning of sequence) 。

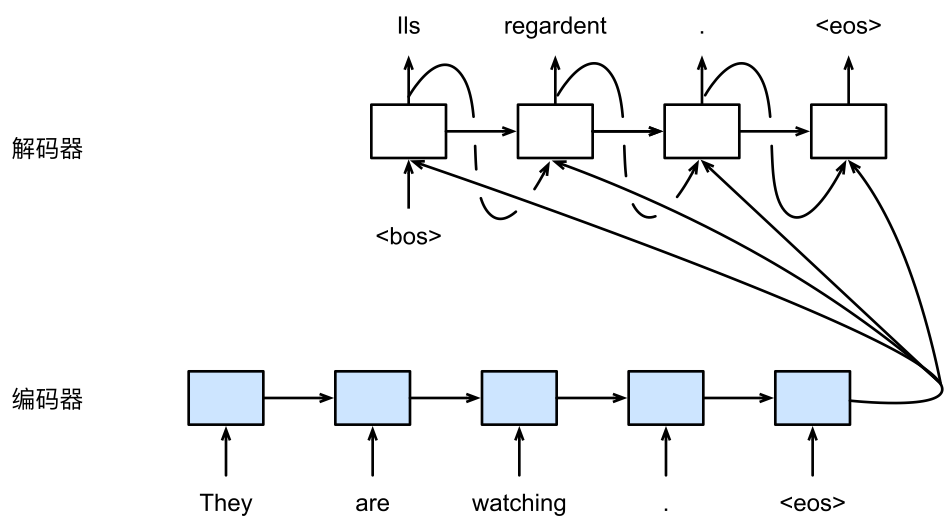
接下来我们介绍编码器和解码器的定义。

编码器 Encoder

编码器的作用是把一个不定长的输入序列变换成一个定长的上下文变量 $\boldsymbol{c}$，并在该上下文变量中编码输入序列信息。常用的编码器是循环神经网络。

现在来看一下上一节的示意图中的编码器部分，”They are watching . <eos>” 是输入序列，由右箭头连起来的蓝色方块序列就是 RNN，蓝色方块是 RNN 的隐层节点 (包含了当前时间步的 hidden state)。

让我们考虑批量大小为1的时序数据样本。假设输入序列是 $x_1, \ldots, x_T$ ，例如 $x_i$ 是输入句子中的第 $i$ 个词。在每一个时间步，输入单词 $x_t$ 的词向量 $\boldsymbol{x}_t$ 会做一次矩阵投影 (matrix projection) 加上偏置项，然后用激活函数激活，得到当前时间步的隐藏状态 $\boldsymbol{h}_t$ 。我们可以用下面的公式表达编码器中时间步 $t$ 的隐藏状态 (假设使用 sigmoid 激活函数)：

$\boldsymbol{h}_t = \sigma(W\boldsymbol{x}_t + b)$

在时间步 $t$，循环神经网络将输入 $x_t$ 的特征向量 $\boldsymbol{x}_t$ 和上个时间步的隐藏状态 $\boldsymbol{h}_{t-1}$ 变换为当前时间步的隐藏状态 $\boldsymbol{h}_t$ 。我们可以用函数 $f$ 表达循环神经网络隐藏层的变换：

$\boldsymbol{h}_t = f(\boldsymbol{x}_t, \boldsymbol{h}_{t-1})$

这里特征向量 $\boldsymbol{x}_t$ 既可以是需要学习的词向量，也可以是预训练的词向量。如果使用的是预训练的词向量，我们可以对输入 $x_t$ 的特征向量 $\boldsymbol{x}_t$ 进行 one-hot 编码，直接从预训练的词向量矩阵 $\boldsymbol{E}$ 读出相应编号的行向量。这也是为什么 Embedding layer 被称为 lookup table 的原因；如果想去学习特征向量 $\boldsymbol{x}_t$ 的词向量，定好词向量矩阵 $\boldsymbol{E}$ 的维度，把它当做模型参数去学。

假设输入序列的总时间步数为 $T$ 。接下来编码器通过自定义函数 $q$ 将各个时间步的隐藏状态变换为上下文变量

$\boldsymbol{c} = q(\boldsymbol{h}_1, \ldots, \boldsymbol{h}_T)$

例如，当选择 $q(\boldsymbol{h}_1, \ldots, \boldsymbol{h}_T) = \boldsymbol{h}_T$ 时，上下文变量是输入序列最终时间步的隐藏状态 $\boldsymbol{h}_T$ 。

上下文变量 $\boldsymbol{c}$ 可以认为是输入序列的语义表达，它总结了输入序列的信息，但它不对输入序列直接编码，而是对输入序列对应的隐含状态编码。

上下文变量 $\boldsymbol{c}$ 编码的方式是多种多样的，直接选择最终时间步的隐藏状态是最简单粗暴的，这样的 Encoder 中其实使用了一个正向的 RNN，每个时间步的隐藏状态只取决于该时间步及之前的输入子序列。我们可以用下面的公式来表达正向的 RNN：

$\vec{\boldsymbol{h}_t} = f(\boldsymbol{x}_t, \vec{\boldsymbol{h}_{t-1}})$

除了正向的 RNN，Encoder 中还可以使用反向的 RNN，每个时间步的隐藏状态只取决于该时间步及之后的输入子序列，上下文编码 $\boldsymbol{c}$ 取第一个时间步的隐藏状态。形象地说，假如我们认为向右是正向的话，正向的 RNN 是从左向右扫一遍，反向的 RNN 是从右向左扫一遍。我们可以用下面的公式来表达反向的 RNN：

$\overleftarrow{\boldsymbol{h}_t} = f(\boldsymbol{x}_t, \overleftarrow{\boldsymbol{h}_{t+1}})$

我们也可以使用双向循环神经网络构造编码器。

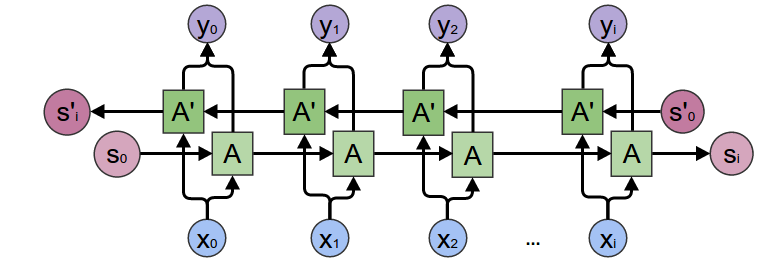
这种情况下，编码器每个时间步的隐藏状态同时取决于该时间步之前和之后的子序列 (包括当前时间步的输入) ，并编码了整个序列的信息。双向 RNN 中，每个时间步的隐藏状态是由该时间步的正向 RNN 隐藏状态和反向 RNN 隐藏状态 concat 起来的。

总之，Encoder 的设计是多种多样的。好，现在我们有了 Encoder 和上下文变量 $\boldsymbol{c}$ ，接下来讲 Decoder 的设计。

解码器 Decoder

刚刚已经介绍，编码器输出的上下文变量 $\boldsymbol{c}$ 编码了整个输入序列 $x_1, \ldots, x_T$ 的信息。解码器通过将上下文变量 $\boldsymbol{c}$ 中的信息解码生成输出序列。给定训练样本中的输出序列 $y_1, y_2, \ldots, y_{T'}$ ，对解码阶段每个时间步 $t’$ ，解码器输出 $y_{t'}$ 的条件概率将基于之前的输出序列 $y_1, \ldots, y_{t'-1}$ 和上下文变量 $\boldsymbol{c}$ ，即 $\mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c})$ 。用下面的公式表示输出序列的联合概率函数：

$\begin{aligned} \mathbb{P}(y_1, \ldots, y_{T'} \mid x_1, \ldots, x_T) &= \prod_{t'=1}^{T'} \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c}) \end{aligned}$

那么，基于之前时间的输出序列 $y_1, \ldots, y_{t'-1}$ 和输入序列的表达 $\boldsymbol{c}$ 如何构造解码器当前时间步的输出 $y_{t'}$ ？

我相信大家已经想到了，可以使用另一个循环神经网络作为解码器，因为 RNN 的结构决定了她很适合基于之前时间的信息来构建当前时间步的输出。

我们的目标是得到一个概率最高的输出序列，因为概率越高表明这个输出序列可能越合理。换句话说，我们想要最大化输出序列的联合概率，根据最大似然估计 (MLE)，最大化这个联合概率与最小化其负对数是等价的。

$\max \mathbb{P}(y_1, \ldots, y_{T'}) \Leftrightarrow \min - log\mathbb{P}(y_1, \ldots, y_{T'})$

联合概率的负对数其实就是交叉熵损失函数，有了损失函数，我们就可以使用优化方法来学习模型参数。这在下一节模型训练中会提到。

解码器的每一个时间步的隐层节点都会有3个输入，分别是上一时间步的输出 $y_{t^\prime-1}$ ，上下文变量 $\boldsymbol{c}$ 以及上一时间步的隐藏状态 $\boldsymbol{s}_{t^\prime-1}$ 。当前时间步的输出 $y_{t^\prime}$ 会作为下一个时间步的输入，这个一个递归的过程，直到生成输出序列停止。于是，我们可以用函数 $p$ 来表达当前时间步的解码器输出概率 $\mathbb{P}$ ：

$\mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c}) = p(y_{t^\prime-1}, \boldsymbol{s}_{t^\prime}, \boldsymbol{c})$

将上一时间步的隐藏状态 $\boldsymbol{s}_{t^\prime-1}$ 做一个矩阵投影 (projection) 再做一次 softmax 即可得到上一时间步的输出 $y_{t^\prime-1}$ ，上下文变量 $\boldsymbol{c}$ 的构造在编码器一节已经讲了，那么解码器中的隐藏状态 $\boldsymbol{s}_{t^\prime}$ 如何得到呢？

在输出序列的时间步 $t^\prime$ ，解码器将上一时间步的输出 $y_{t^\prime-1}$ 以及上下文变量 $\boldsymbol{c}$ 作为输入，并将它们与上一时间步的隐藏状态 $\boldsymbol{s}_{t^\prime-1}$ 变换为当前时间步的隐藏状态 $\boldsymbol{s}_{t^\prime}$ 。因此，我们可以用函数 $g$ 表达解码器隐藏层的变换：

$\boldsymbol{s}_{t^\prime} = g(y_{t^\prime-1}, \boldsymbol{c}, \boldsymbol{s}_{t^\prime-1})$

现在， $g$ 函数的设计变成了解码器设计的关键，在 Bahanau 等人的第一篇关于注意力机制的论文中这个 $g$ 函数就是 GRU，它的具体实现会在后面的注意力机制一节中给出一个案例。

有了解码器的隐藏状态后，我们可以使用自定义的输出层和 softmax 运算来计算 $\mathbb{P}(y_{t^\prime} \mid y_1, \ldots, y_{t^\prime-1}, \boldsymbol{c})$ ，就像之前提到的基于当前时间步的解码器隐藏状态 $\boldsymbol{s}_{t^\prime}$ 、上一时间步的输出 $y_{t^\prime-1}$ 以及上下文变量 $\boldsymbol{c}$ 来计算当前时间步输出 $y_{t^\prime}$ 的概率分布。

模型训练 Model Training

根据最大似然估计，我们可以最大化输出序列基于输入序列的条件概率

$\begin{aligned} \mathbb{P}(y_1, \ldots, y_{T'} \mid x_1, \ldots, x_T) &= \prod_{t'=1}^{T'} \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, x_1, \ldots, x_T)\\ &= \prod_{t'=1}^{T'} \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c}) \end{aligned}$

并得到该输出序列的损失

$\log\mathbb{P}(y_1, \ldots, y_{T'} \mid x_1, \ldots, x_T) = -\sum_{t'=1}^{T'} \log \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c})$

在模型训练中，我们通过最小化这个损失函数来得到模型参数。

模型预测 Model Prediction

上一节介绍了如何训练输入输出均为不定长序列的编码器—解码器，这一节我们介绍如何使用编码器—解码器来预测不定长的序列。

上一节里已经提到，在准备训练数据集时，我们通常会在样本的输入序列和输出序列后面分别附上一个特殊符号 “<eos>” 表示序列的终止。我们在接下来的讨论中也将沿用上一节的数学符号。为了便于讨论，假设解码器的输出是一段文本序列。设输出文本词典 $\mathcal{Y}$ (包含特殊符号“<eos>”) 的大小为 $\left|\mathcal{Y}\right|$ ，输出序列的最大长度为 $T’$ 。所有可能的输出序列一共有 $\mathcal{O}(\left|\mathcal{Y}\right|^{T’})$ 种。这些输出序列中所有特殊符号“<eos>”后面的子序列将被舍弃。

穷举搜索 Exhaustive Search

我们在上一节描述解码器时提到，输出序列基于输入序列的条件概率是 $\prod_{t'=1}^{T'} \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c})$ 。为了搜索该条件概率最大的输出序列，一种方法是穷举所有可能输出序列的条件概率，并输出条件概率最大的序列。我们将该序列称为最优序列，并将这种搜索方法称为穷举搜索 (exhaustive search)。

虽然穷举搜索可以得到最优序列，但它的计算开销 $\mathcal{O}(\left|\mathcal{Y}\right|^{T’})$ 很容易过大。例如，当 $|\mathcal{Y}|=10000$ 且 $T’=10$ 时，我们将评估 $10000^{10} = 10^{40}$ 个序列：这几乎不可能完成。

贪婪搜索 Greedy Search

我们还可以使用贪婪搜索 (greedy search) 。也就是说，对于输出序列任一时间步 $t’$，从 $|\mathcal{Y}|$ 个词中搜索出输出词

$y_{t'} = \text{argmax}_{y_{t'} \in \mathcal{Y}} \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c})$

且一旦搜索出 “<eos>” 符号即完成输出序列。贪婪搜索的计算开销是 $\mathcal{O}(\left|\mathcal{Y}\right|T’)$。它比起穷举搜索的计算开销显著下降。例如，当 $|\mathcal{Y}|=10000$ 且 $T’=10$ 时，我们只需评估 $10000\times10=1\times10^5$ 个序列。

下面我们来看一个例子。假设输出词典里面有 “A”、“B”、“C”和 “<eos>” 这四个词。下图中每个时间步下的四个数字分别代表了该时间步生成 “A”、“B”、“C”和 “<eos>” 这四个词的条件概率。在每个时间步，贪婪搜索选取生成条件概率最大的词。因此，将生成序列 “ABC<eos>” 。该输出序列的条件概率是 $0.5\times0.4\times0.4\times0.6 = 0.048$。

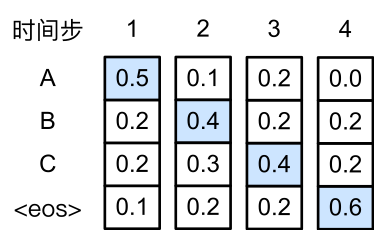
正如绝大部分贪婪算法不能保证最优解一样，贪婪搜索也无法保证找出条件概率最大的最优序列。下图演示了这样的一个例子。与上图中不同，下图在时间步2中选取了条件概率第二大的 “C” 。由于时间步3所基于的时间步1和2的输出子序列由上图中的 “AB” 变为了下图中的 “AC”，下图中时间步3生成各个词的条件概率发生了变化。我们选取条件概率最大的 “B”。此时时间步4所基于的前三个时间步的输出子序列为 “ACB”，与上图中的 “ABC” 不同。因此下图时间步4生成各个词的条件概率也与上图中的不同。我们发现，此时的输出序列 “ACB<eos>” 的条件概率是$0.5\times0.3\times0.6\times0.6=0.054$，大于贪婪搜索得到的输出序列的条件概率。因此，贪婪搜索得到的输出序列 “ABC<eos>” 并非最优序列。

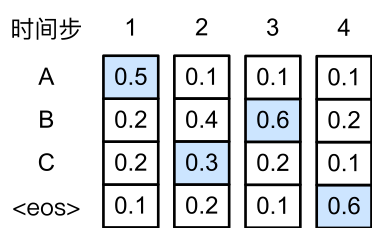
束搜索 Beam Search

束搜索 (beam search) 是比贪婪搜索更加广义的搜索算法。它有一个束宽 (beam size) 超参数。我们将它设为 $k$。在时间步1时，选取当前时间步生成条件概率最大的 $k$ 个词，分别组成 $k$ 个候选输出序列的首词。在之后的每个时间步，基于上个时间步的 $k$ 个候选输出序列，从 $k\left|\mathcal{Y}\right|$ 个可能的输出序列中选取生成条件概率最大的 $k$ 个，作为该时间步的候选输出序列。
最终，我们在各个时间步的候选输出序列中筛选出包含特殊符号 “<eos>” 的序列，并将它们中所有特殊符号 “<eos>” 后面的子序列舍弃，得到最终候选输出序列。在这些最终候选输出序列中，取以下分数最高的序列作为输出序列：

$\frac{1}{L^\alpha} \log \mathbb{P}(y_1, \ldots, y_{L}) = \frac{1}{L^\alpha} \sum_{t'=1}^L \log \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c})$

其中 $L$ 为最终候选序列长度，$\alpha$ 一般可选为0.75。分母上的 $L^\alpha$ 是为了惩罚较长序列在以上分数中较多的对数相加项。分析可得，束搜索的计算开销为 $\mathcal{O}(k\left|\mathcal{Y}\right|T’)$。这介于穷举搜索和贪婪搜索的计算开销之间。

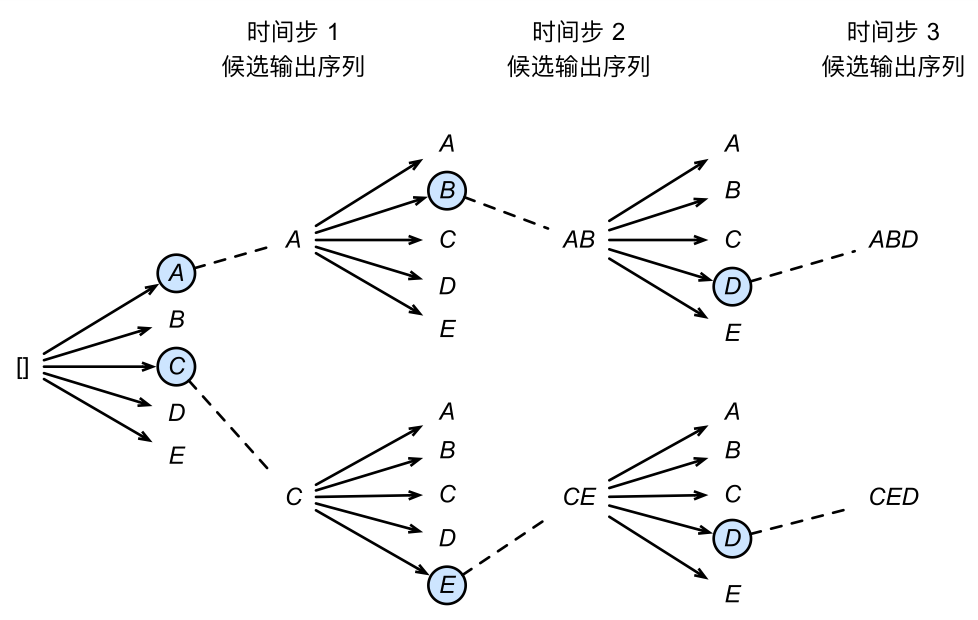
上图通过一个例子演示了束搜索的过程。假设输出序列的词典中只包含五个元素：$\mathcal{Y} = {A, B, C, D, E}$，且其中一个为特殊符号 “<eos>”。设束搜索的束宽等于2，输出序列最大长度为3。在输出序列的时间步1时，假设条件概率 $\mathbb{P}(y_1 \mid \boldsymbol{c})$ 最大的两个词为 $A$ 和 $C$。我们在时间步2时将对所有的 $y_2 \in \mathcal{Y}$ 都分别计算 $\mathbb{P}(y_2 \mid A, \boldsymbol{c})$ 和 $\mathbb{P}(y_2 \mid C, \boldsymbol{c})$，并从计算出的10个条件概率中取最大的两个：假设为 $\mathbb{P}(B \mid A, \boldsymbol{c})$ 和$\mathbb{P}(E \mid C, \boldsymbol{c})$。那么，我们在时间步3时将对所有的 $y_3 \in \mathcal{Y}$ 都分别计算 $\mathbb{P}(y_3 \mid A, B, \boldsymbol{c})$ 和 $\mathbb{P}(y_3 \mid C, E, \boldsymbol{c})$，并从计算出的10个条件概率中取最大的两个：假设为 $\mathbb{P}(D \mid A, B, \boldsymbol{c})$ 和 $\mathbb{P}(D \mid C, E, \boldsymbol{c})$。接下来，我们可以在6个候选输出序列：$A$、$C$、$AB$、$CE$、$ABD$和$CED$中筛选出包含特殊符号“<eos>”的序列，并将它们中所有特殊符号“<eos>”后面的子序列舍弃，得到最终候选输出序列。我们可以在最终候选输出序列中取分数最高的序列作为输出序列。

贪婪搜索可看作是束宽为1的束搜索。束搜索通过更灵活的束宽 $k$ 来权衡计算开销和搜索质量。

技巧 Tricks

1.When stop? 在模型预测的时候，解码器可以一直生成序列，何时停止呢？

我们会在训练数据集中加入 <eos> ，表示序列的结束。如果输出序列中出现 <eos> ，生成停止。

2.Eecoder 中，初始时刻的隐层节点输入 $h_0$ 是什么？

零向量。

3.Decoder 中，初始时刻的隐层节点输入 $y_0$ 是什么？

<bos> ，表示序列的开始。它是一个词向量，通过训练过程学出来。

4.Decoder 中，初始时刻的隐藏状态 $s_0$ 如何初始化？

最简单的就是初始化为零向量。但，我们有时候希望 $s_0$ 能够看到输入序列的信息。比如在机器翻译任务中，解码器第一个时间步的隐藏状态看起来似乎会与输入序列的第一个词的信息有关。在 Bahanau 等人的注意力机制文章中，是这么初始化的：

$s_0 = tanh(W \overleftarrow{h_1})$

Encoder 中使用了一个反向的 RNN，将第一个时间步的隐藏状态 $\overleftarrow{h_1}$ 做一次矩阵投影，再用 $tanh$ 激活函数激活，得到 $s_0$ 。通俗地将，就是把第一个词的信息丢给了 $s_1$ ，让模型去翻译好第一个词。

注意力机制 Attention Mechanism

在”编码器—解码器”一节里的解码器设计中，输出序列的各个时间步使用了相同的上下文变量。换句话说，解码阶段不同时间步看到的输入序列的信息都是一样的，这可能是模型的一个瓶颈。如果解码器的不同时间步可以使用不同的上下文变量呢？这样做有什么好处？

动机 Motivation

以英语-法语翻译为例，给定一对英语输入序列 “They”、“are”、“watching”、“.” 和法语输出序列 “Ils”、“regardent”、“.”。解码器可以在输出序列的时间步1使用更集中编码了 “They”、“are” 信息的上下文变量来生成 “Ils”，在时间步2使用更集中编码了 “watching” 信息的上下文变量来生成“regardent”，在时间步3使用更集中编码了 “.” 信息的上下文变量来生成 “.”。这看上去就像是在解码器的每一时间步对输入序列中不同时间步编码的信息分配不同的注意力。这也是注意力机制的由来。它最早由 Bahanau 等人提出。

设计 Design

本节沿用”编码器—解码器”一节里的数学符号。

我们对”编码器—解码器”一节里的解码器稍作修改。在时间步 $t’$，解码器的上下文变量从原来的 $\boldsymbol{c}$ 泛化了，设为 $\boldsymbol{c}_{t'}$ ，输出 $y_{t'}$ 的特征向量为 $\boldsymbol{y}_{t'}$ 。

和输入的特征向量一样，这里每个输出的特征向量也是模型参数。解码器在时间步 $t’$ 的隐藏状态的计算也发生了改变：

$\boldsymbol{s}_{t'} = g(\boldsymbol{y}_{t'-1}, \boldsymbol{c}_{t'}, \boldsymbol{s}_{t'-1})$

那么 $\boldsymbol{c}_{t'}$ 如何设计？就像之前提到的，注意力机制的目标是让解码器在每一时间步对输入序列中不同时间步编码的信息分配不同的注意力。那么体现在上下文变量中， $\boldsymbol{c}_{t'}$ 就是 Encoder 中不同时间步的隐藏状态的加权平均。

令编码器在时间步 $t$ 的隐藏状态为 $\boldsymbol{h}_t$，且总时间步数为 $T$。解码器在时间步 $t’$ 的上下文变量为

$\boldsymbol{c}_{t'} = \sum_{t=1}^T \alpha_{t' t} \boldsymbol{h}_t$

其中 $\alpha_{t’ t}$ 是权值。也就是说，给定解码器的当前时间步 $t’$，我们需要对编码器中不同时间步 $t$ 的隐藏状态求加权平均。说到加权平均，我们很容易想到 softmax 函数。这里的权值也称注意力权重。它的计算公式是

$\alpha_{t' t} = \frac{\exp(e_{t' t})}{ \sum_{k=1}^T \exp(e_{t' k}) }$

其中 $e_{t’ t} \in \mathbb{R}$ 的计算为

$e_{t' t} = a(\boldsymbol{s}_{t' - 1}, \boldsymbol{h}_t)$

上式中的函数 $a$ 就是注意力函数，有多种设计方法。Bahanau 等使用了多层感知机：

$e_{t' t} = \boldsymbol{v}^\top \tanh(\boldsymbol{W}_s \boldsymbol{s}_{t' - 1} + \boldsymbol{W}_h \boldsymbol{h}_t)$

其中 $\boldsymbol{v}$、$\boldsymbol{W}_s$、$\boldsymbol{W}_h$ 以及编码器与解码器中的各个权重和偏差都是模型参数。

在解码器一节中，讲到了解码器设计的关键就在于那个 $g$ 函数， $g$ 函数的三个输入参数 $\boldsymbol{y}_{t'-1}, \boldsymbol{c}_{t'}, \boldsymbol{s}_{t'-1}$ 如何描述？现在我们来看它的一个具体设计，变种 RNN：GRU。

Bahanau 等在编码器和解码器中分别使用了门控循环单元 GRU。在解码器中，我们需要对门控循环单元的设计稍作修改。解码器在 $t’ $ 时间步的隐藏状态为

$\boldsymbol{s}_{t'} = \boldsymbol{z}_{t'} \odot \boldsymbol{s}_{t'-1} + (1 - \boldsymbol{z}_{t'}) \odot \tilde{\boldsymbol{s}}_{t'}$

其中的重置门、更新门和候选隐含状态分别为

$\begin{aligned} \boldsymbol{r}_{t'} &= \sigma(\boldsymbol{W}_{yr} \boldsymbol{y}_{t'-1} + \boldsymbol{W}_{sr} \boldsymbol{s}_{t' - 1} + \boldsymbol{W}_{cr} \boldsymbol{c}_{t'} + \boldsymbol{b}_r),\\ \boldsymbol{z}_{t'} &= \sigma(\boldsymbol{W}_{yz} \boldsymbol{y}_{t'-1} + \boldsymbol{W}_{sz} \boldsymbol{s}_{t' - 1} + \boldsymbol{W}_{cz} \boldsymbol{c}_{t'} + \boldsymbol{b}_z),\\ \tilde{\boldsymbol{s}}_{t'} &= \text{tanh}(\boldsymbol{W}_{ys} \boldsymbol{y}_{t'-1} + \boldsymbol{W}_{ss} (\boldsymbol{s}_{t' - 1} \odot \boldsymbol{r}_{t'}) + \boldsymbol{W}_{cs} \boldsymbol{c}_{t'} + \boldsymbol{b}_s). \end{aligned}$

重置门和更新门中都体现了 $g$ 函数的三个输入参数，重置门用于控制隐藏状态的流动，换句话说，控制记忆。值得注意的是，候选隐藏含量中的 $\odot$ 是逐点相乘器，上下文变量 $\boldsymbol{c}_{t'}$ 并不参与门控。有了候选隐含变量 $\tilde{\boldsymbol{s}}_{t'}$ 之后，通过更新门 $\boldsymbol{z}_{t'}$ 控制信息，得到隐含变量 $\boldsymbol{s}_{t'}$ 。

到这里，Seq2Seq 和 Attention Mechanism 就讲完了！Seq2Seq (Encoder-Decoder) 模型的构思还是很巧妙的，能够处理输入序列和输出序列都是不定长的问题。

总结 Conclusions

让我们回顾一下带注意力机制的编码器-解码器的整个设计：

Encoder 总结输入序列的信息，得到上下文变量 $\boldsymbol{c}$
Decoder 将上下文变量中的信息解码生成输出序列
1. 设计 $g$ 函数
2. 计算当前时间步的隐藏状态 $\boldsymbol{s}_{t^\prime}$
3. 计算当前时间步的解码器输出概率 $\mathbb{P}(y_{t^\prime})$
4. 得到输出序列的联合概率 $\mathbb{P}(y_1, \ldots, y_{T'})$ 并最大化
5. 根据 MLE，就是最小化联合概率的负对数
6. 得到 loss function
7. 用优化方法降低 loss，学习模型参数
为了避免相同的上下文变量对模型性能的限制，给编码器-解码器模型加入了注意力机制。

思考题

1.除了机器翻译 (Neural Machine Translation)，你还能想到 seq2seq 的哪些应用？

答：

文本摘要 Text Summarization
图像描述 Image Captioning
语法纠错 Grammar Error Correction
对话生成
自动邮件回复
诗词生成、歌词生成
生成 git commit message
生成代码补全

Seq2Seq 主要可以用于自然语言生成。

自然语言生成 (NLG) 是一个非常有意思的研究领域，简单地说就是解决一个条件概率 P(output | context) 的建模问题，根据上下文来生成文本，这里的 context 可以做很多文章，对于生成文本的控制 (Seq2Seq 中的 Decoding 部分) 也可以做很多文章，anyway，利用 Seq2Seq 可以实现很多有趣的工作。

2.有哪些方法可以设计解码器的输出层？

答：最简单就是 RNN 每个隐层节点的输出 + Softmax

3.为什么 seq2seq 的 loss function 选择交叉熵损失函数？除了交叉熵损失函数，还可以有哪些选择？

答：seq2seq 在生成输出序列的时候是一个时刻生成一项，换句话说，在每个时间步他在解决一个分类问题。

而交叉熵损失函数是分类问题中最常用的损失函数，当然，如果 seq2seq 试图解决一个回归问题，我们可以使用别的损失函数，比如 L2 loss。

4.穷举搜索可否看做是特殊束宽的束搜索？为什么？

答：不能。穷举搜索在每个时间步并没有一个“束宽”来限制候选项的个数。

5.除了自然语言处理，注意力机制还可以应用在哪些地方？

答：CV, Speech and More。

Attention 机制的思想在于给模型引入了新的非线性操作。

传统 CNN 架构里非线性操作只有 max pooling 和非线性激活函数。虽说理论上只用这俩去拟合复杂函数仍然是可行的，但是会比较困难，且参数量巨大。相反，如果直接给一个与目标函数相近的非线性函数来作为函数线性组合的一个基，就方便很多了。

References

编码器-解码器，GLUON 动手学深度学习
MXNet/Gluon 中文频道，动手学深度学习第十八课：seq2seq（编码器和解码器）和注意力机制
multiangle, Encoder-Decoder模型和Attention模型
Goodfellow I, Bengio Y, Courville A, et al. Deep learning[M]. Cambridge: MIT press, 2016.
Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
Sutskever, I., Vinyals, O., & Le, Q. V. (2014). Sequence to sequence learning with neural networks. In Advances in neural information processing systems (pp. 3104-3112).
Bahdanau et al., Neural Machine Translation by Jointly Learning to Align and Translate
Andrej Karpathy, The Unreasonable Effectiveness of Recurrent Neural Networks
Christopher Olah, Understanding LSTM Networks