交叉验证的原理及实现

Posted on | In | |

最近在写一个层次分类模型，为了更好地选择模型，用到了交叉验证，于是详细了解了一下。

介绍

交叉验证一般应用于样本数据不充足的情况下，它的基本想法就是重复地使用数据：把给定的数据进行切分，将切分的数据集组合为训练集和测试集，在此基础上反复地进行训练、测试以及模型选择。

交叉验证的目的是为了能有效地估计模型的泛化能力 (测试误差)，从而进行模型选择。

交叉验证方法

保留交叉验证 hand-out cross validation

首先随机地将已给数据分为两部分：训练集和测试集 (例如，70% 训练集，30% 测试集)；

然后用训练集在各种条件下 (比如，不同的参数个数) 训练模型，从而得到不同的模型；

在测试集上评价各个模型的测试误差，选出测试误差最小的模型。

这种方式其实严格意义上并不能算是交叉验证，因为训练集的样本数始终是那么多，模型并没有看到更多的样本，没有体现交叉的思想。

由于是随机的将原始数据分组，所以最后测试集上准确率的高低与原始数据的分组有很大的关系，所以这种方法得到的结果其实并不具有说服性。

k折交叉验证 k-fold cross validation

这是应用最多的交叉验证方式。

首先随机地将数据集切分为 k 个互不相交的大小相同的子集；

然后将 k-1 个子集当成训练集训练模型，剩下的 (held out) 一个子集当测试集测试模型；

将上一步对可能的 k 种选择重复进行 (每次挑一个不同的子集做测试集)；

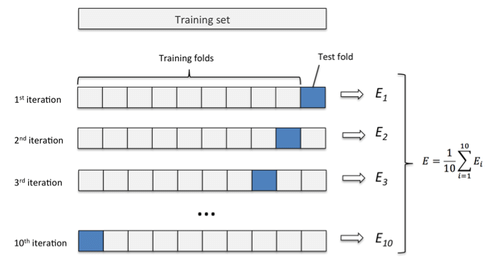
这样就训练了 k 个模型，每个模型都在相应的测试集上计算测试误差，得到了 k 个测试误差，对这 k 次的测试误差取平均便得到一个交叉验证误差。这便是交叉验证的过程。

计算平均测试误差 (交叉验证误差) 来评估当前参数下的模型性能。

在模型选择时，假设模型有许多 tuning parameter 可供调参，一组 tuning parameter 便确定一个模型，计算其交叉验证误差，最后选择使得交叉验证误差最小的那一组 tuning parameter。这便是模型选择过程。

k 一般大于等于2，实际操作时一般从3开始取，只有在原始数据集样本数量小的时候才会尝试取2。

k折交叉验证可以有效的避免过拟合以及欠拟合状态的发生，最后得到的结果也比较具有说服性。

k折交叉验证最大的优点：

  • 所有数据都会参与到训练和预测中，有效避免过拟合，充分体现了交叉的思想

交叉验证可能存在 bias 或者 variance。如果我们提高切分的数量 k，variance 会上升但 bias 可能会下降。相反得，如果降低 k，bias 可能会上升但 variance 会下降。bias-variance tradeoff 是一个有趣的问题，我们希望模型的 bias 和 variance 都很低，但有时候做不到，只好权衡利弊，选取他们二者的平衡点。

通常使用10折交叉验证，当然这也取决于训练数据的样本数量。

10-fold cross validation:

10-fold cv

留一交叉验证 leave-one-out cross validation

k折交叉验证的特殊情况，k=N，N 是数据集的样本数量，往往在数据缺乏的情况下使用。

留一交叉验证的优点是：

  • 每一回合中几乎所有的样本皆用于训练模型，因此最接近原始样本的分布，这样评估所得的结果比较可靠。
  • 实验过程中没有随机因素会影响实验数据，确保实验过程是可以被复制的。

缺点是：

  • 计算成本高，因为需要建立的模型数量和原始数据集样本数量一致，尤其当样本数量很大的时候。可以考虑并行化训练模型减少训练时间。

总之，交叉验证对于我们选择模型以及模型的参数都是很有帮助的。

但以上交叉验证的方法都有一个问题，就是在数据分组的时候缺乏随机性，以 k折交叉验证 为例，每个数据样本只能固定属于 k 个子集中的一个，可能会造成对于最终结果的影响。于是有人提出了 bootstrapping。

Bootstrapping

cv 和 bootstrapping 都是重采样 (resampling) 的方法。机器学习中常用的 bagging 和 boosting 都是 bootstrapping 思想的应用。

bootstrapping 的思想是依靠自己的资源，称为自助法，它是一种有放回的抽样方法。

bootstrapping 的过程如下：

  1. 数据假设要分成10组，则先设置一个采样比例，比如采样比例70%。则10组数据是每次从原始数据集中随机采样总数70%的数据构成训练集1，没有选中的样本作为测试集1；然后把数据放回，再随机采样总数70%的数据构成训练集2，没选中的作为测试集2……以此类推，放回式采样10组。
  2. 训练生成10个模型
  3. 计算平均测试误差来评估当前参数下的模型性能

除此之外，bootstrapping 在集成学习方法中也很有用。比如我们可以用经过 bootstrapping 的多组数据集构建模型 (比如决策树)，然后将这些模型打包 (bag，就像随机森林)，最后使用这些模型的最大投票结果作为我们最终的输出。

用 sklearn 实现交叉验证

莺尾花分类问题，使用5折交叉验证

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.cross_validation import cross_val_score

def cv_train():
    iris = load_iris()
    X = iris.data
    y = iris.target
    X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=4)

    knn = KNeighborsClassifier(n_neighbors=5)
    knn.fit(X_train, y_train)
    scores = cross_val_score(knn, X, y, cv=5, scoring='accuracy')
    print(scores)    # [0.96666667 1.         0.93333333 0.96666667 1.        ]
    print(scores.mean())    # 0.9733333333333334

if __name__ == '__main__':
    cv_train()

有了交叉验证，通过指定不同的模型参数 (上面的 knn 的参数就是 n_neighbors)，计算平均测试误差 (当然评估指标是根据问题的类型而定，acc 用于分类模型，mse 用于回归模型)，指标最好的模型对应的参数就是我们要选择的模型参数。

对于一些复杂的自定义的模型，数据集的读取并不是 sklearn 风格的，比如我最近写的一个层次分类模型，每一个层中每一个分类器的数据读取都是要到特征配置文件中找到对应的特征组再去数据集中读出来，这样很难使用 sklearn 的接口，于是我自己写了一个切分数据集的函数，来进行交叉验证。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def kfold_split(dataset, k_splits):
    """
    Split the dataset into k folds
    Args:
        dataset: the list of sample features
        k_splits: the number of folds
    """
    assert len(dataset) > 0, 'Dataset is empty!'
    cv_dataset_list = []    # [(trainset_1, testset_1), ..., (trainset_k, testset_k)]
    
    # chunk the dataset into k folds
    dataset_size = len(dataset)
    fold_size = dataset_size / float(k_splits)
    chunked_dataset = []
    last = 0.0
    split_counter = 1
    while split_counter <= k_splits:
        chunked_dataset.append(dataset[int(last):int(last + fold_size)])
        last += fold_size
        split_counter += 1
    assert len(chunked_dataset) == k_splits, 'The size of chunked_dataset should be same as k_splits!'
    
    for index in range(k_splits):
        testset = chunked_dataset[index]
        trainset = []
        for i in range(k_splits):
            if i == index:
                continue
            trainset += chunked_dataset[i]

        train_test = (trainset, testset)
        cv_dataset_list.append(train_test)
    return cv_dataset_list

k 折切分数据集后，在包含 k 个 (训练集，测试集) 组的列表中逐一训练、测试模型，得到 k 个模型，最后计算这些模型的平均测试误差，这样就完成了一次交叉验证。

References

  • 李航，统计学习方法
  • Cross Validation, Wikipedia
  • 交叉验证，莫烦Python
资磁一下？