LDA 数学笔记

LDA 主题模型几乎是每一个 NLP 工程师的必修课，而她背后的数学与概率论知识却让她看起来有些高冷。

那么何为 LDA (Latent Dirichlet Allocation)？

简单的说，L (Latent 隐含)，主题隐含在文档中；DA (Dirichlet Allocation 狄利克雷分布)，文档的主题服从 Dirichlet Distribution。

本文将站在一个初学者的角度来讲述 LDA 与她背后的故事。

---

介绍 Introduction

人类通过先验知识和上下文来理解文档 (Document) 中的主题 (Topic)，这对人类来说很容易，但是对机器而言难度就大了很多。

LDA (Latent Dirichlet Allocation) 通过建立一种

• 词袋模型 (Bag-of-Word Model)：一篇文档是由一组词构成的一个集合，词与词之间没有顺序以及先后的关系
• 统计模型 (Statistical Model)：经过数理统计法求得各变量之间的函数关系
• 生成概率模型 (Generative Probabilistic Model)：认为每一类数据都服从某一种分布，如狄利克雷分布
• 主题模型 (Topic Model)：在机器学习和自然语言处理等领域，用来在一系列文档中发现抽象主题的一种统计模型
• 无监督学习模型 (Unsupervised Model)：在训练时不需要人工标注的数据集，需要的仅仅是文档集以及指定主题的数量 K

来发现文档集 (Document Collection / Corpus) 中的抽象主题，从而试图解决这类问题。

在机器学习领域中有2个 LDA：

• 线性判别分析 (Linear Discriminant Analysis)，主要用于降维和分类。
• 隐含狄利克雷分布 (Latent Dirichlet Allocation)，在主题模型中占有重要的地位，目前在文本挖掘领域包括文本主题识别、文本分类以及文本相似度计算方面都有应用。

本文关注的是后者。

LDA 由 Blei, David M., Andrew Y. Ng, and Michael I. Jordan 于 2003 年提出，可以将文档集中每篇文档的主题按照概率分布的形式给出。

那么何为 LDA？

简单得说，L (Latent 隐含)，主题隐含在文档中；DA (Dirichlet Allocation 狄利克雷分布)，文档的主题服从狄利克雷分布 (Dirichlet Distribution)。

---

提纲 Outline

为了深入理解 LDA 主题模型，我们需要了解下列5个部分：

• 一个概念：贝叶斯定理
• 一个函数：Gamma 函数
• 五个分布：二项分布 <-> Beta 分布，多项分布 <-> Dirichlet 分布，共轭分布
• 两个模型：PLSA 模型，LDA 模型
• 两个算法：变分推断之 EM 算法，Gibbs 采样算法 (马尔科夫链蒙特卡罗 MCMC)

让我们先从直觉出发，从一种宏观的角度看 LDA。

---

直觉 Intuition behind LDA

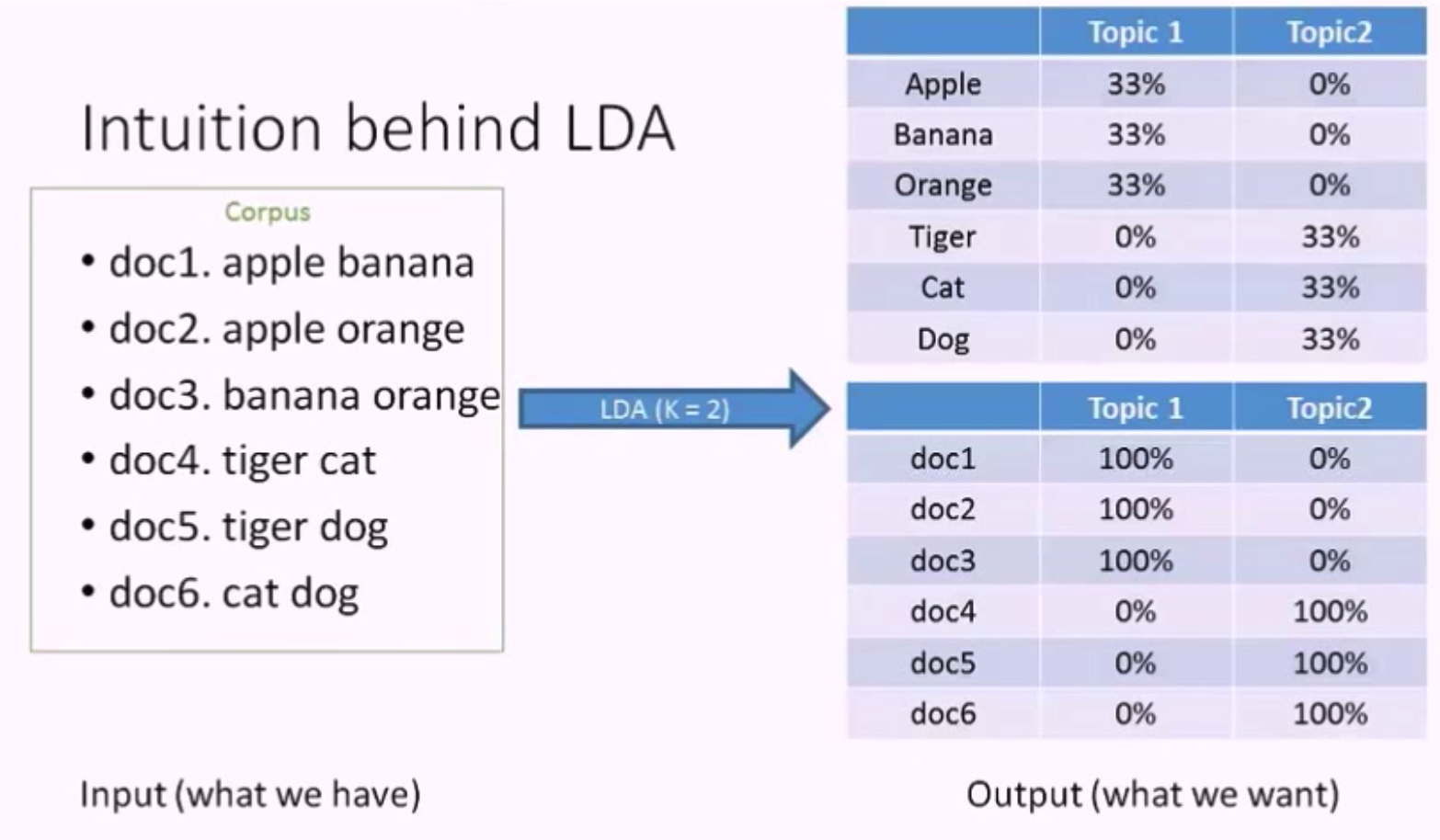
现在我们有六篇文档，如上图所示，前三篇的主题是关于水果的，后三篇是关于动物的。

假如将这六篇文档作为 LDA 模型的输入，并且设 K = 2，这里的 K 是 LDA 模型中的一个重要参数，代表我们想从文档集中抽取出的主题的数量。

LDA 的第一个输出是主题的单词分布 (Topic - Word Distribution)，由上图可知，主题1的单词概率分布是 apple banana orange 各占 33%，这就是 LDA 描述主题的方法，她使用单词 (Word / Term) 来描述主题。

LDA 的第二个输出是文档的主题分布 (Doc - Topic Distribution)，由上图可知，文档1中单词 apple banana 都是关于水果的，所以它的主题是 100% 关于主题1 (水果)，文档4的主题是 100% 关于主题2 (动物)。当然，一个文档中是可以包含多个主题的，此处的例子只包含一个主题是因为文档中单词比较少，正好都关于一个主题。

让我们梳理一下，LDA 的输入是一个文档集，输出是2个分布，基本上她会告诉你 每个主题在讨论什么 以及 每篇文档中包含了哪些主题。

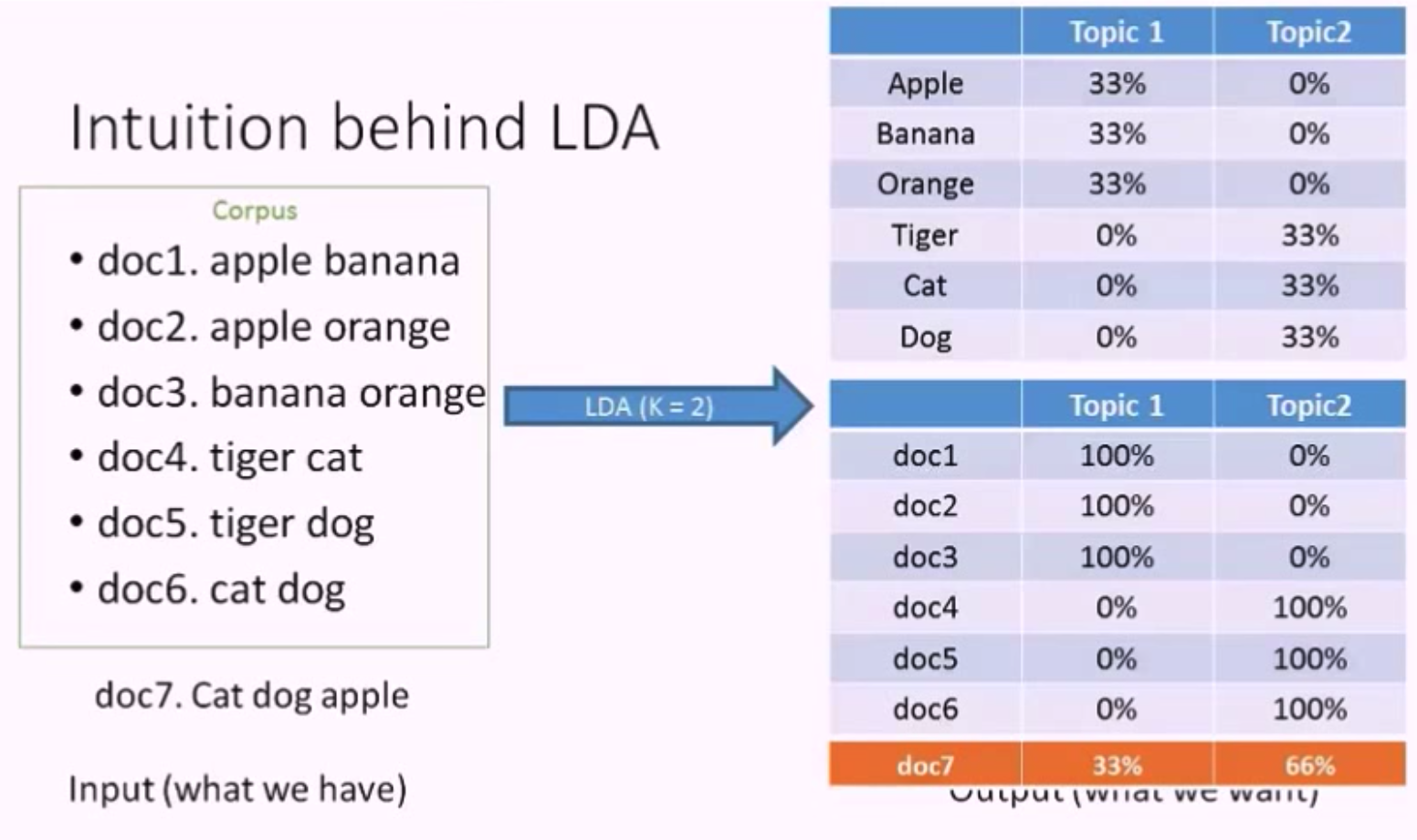
有了 LDA 的输出结果，我们可以对新文档的主题进行预测。

假如我们现在有一个新文档 doc7. cat dog apple，可以预测出它的主题分布是 33% 关于主题1，66% 关于主题2。

好，现在我们直观地感受了一下 LDA 模型的输入输出以及她预测新文档主题分布的能力，那她的模型结构和求解原理是怎么样的呢？

要想理解她的原理，我们需要了解在 LDA 中，一篇文档的生成过程以及其逆过程，这个逆过程就是求解文档的主题分布的过程。

在深入讲解她之前，我们需要一些先验知识作为铺垫。

---

贝叶斯定理 Bayes Theorem

$$P(A|B)=\frac{P(A)\times{P(B|A)}}{P(B)}$$ $$posterior = prior \times likelihood$$ $$后验概率 = 先验概率 \times 似然$$

• 概率: 用于在已知一些参数的情况下，预测接下来的观测所得到的结果。
• 似然: 用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。
• $P(A|B)$: 是已知 B 发生后 A 的条件概率，也由于得自B的取值而被称作 A 的后验概率。
• $P(A)$: 是 A 的先验概率。之所以称为”先验”是因为它不考虑任何 B 方面的因素。
• $P(B|A)$: 是已知 A 发生后 B 的条件概率，也由于得自A的取值而被称作 B 的后验概率。
• $P(B)$: 是 B 的先验概率。
• $\frac{P(B|A)}{P(B)}$: 称作标准似然 (standardised likelihood)

举个好人坏人的例子，你对好人和坏人的认知，先验分布为：100个好人和100个的坏人，即你认为好人坏人各占一半，现在你被2个好人帮助了和1个坏人骗了 (似然)，于是你得到了新的后验分布为：102个好人和101个的坏人。现在你的后验分布里面认为好人比坏人多了。这个后验分布接着又变成你的新的先验分布，当你被1个好人帮助了和3个坏人骗了后 (似然)，你又更新了你的后验分布为：103个好人和104个的坏人。依次继续更新下去。

LDA 是基于贝叶斯模型的，她是一个三层贝叶斯模型。

---

伽玛函数 Gamma Function

定义：

$$\Gamma(x) = \int_{0}^{\infty}t^{x-1}e^{-t}dt$$

分部积分后，可以发现 Gamma 函数具有这样神奇的性质：

$$\Gamma(x+1) = x \Gamma(x)$$

Gamma 函数可以看成是阶乘在实数集上的延拓：

$$\Gamma(n) = (n-1)!$$

为什么要提到 Gamma 函数？

LDA 所涉及的概率分布中会用到 Gamma 函数以及它的性质，所以先介绍一下 Gamma 函数。

---

一些概率论 Some Probability Theory

LDA 主题模型中涉及了许多概率分布，列举如下。

伯努利分布 Bernoulli Distribution

伯努利试验是只有2种可能结果的单次随机试验。

进行一次伯努利试验，成功 (X=1) 概率为 p (0<=p<=1)，失败 (X=0) 概率是 1-p，则称随机变量 X 服从伯努利分布。

概率密度公式为：

$$f_{X}(x) = p^{x}(1-p)^{1-x} = \begin{cases} p & \text{if} \ x = 1,\\ q & \text{if} \ x = 0. \end{cases}$$

二项分布 Binomial Distribution

是 N 重伯努利分布，X ~ B(n, p).

概率密度公式为：

$$P(K = k) = \begin{pmatrix} n \\ k \\ \end{pmatrix} p^k{(1-p)}^{n-k}$$

多项分布 Multinomial Distribution

多项分布，是二项分布扩展到多维的情况. 多项分布是指单次试验中的随机变量的取值不再是 0-1 的，而是有多种离散值可能（1,2,3…,k）.

概率密度函数为：

$$P(x_1, x_2, ..., x_k; n, p_1, p_2, ..., p_k) = \frac{n!}{x_1!...x_k!}{p_1}^{x_1}...{p_k}^{x_k}$$

贝塔分布 Beta Distribution

Beta分布的定义：对于参数 $\alpha > 0, \beta > 0$ , 取值范围为 [0, 1] 的随机变量 X 的概率密度函数为：

$$f(x; \alpha, \beta) = \frac{1}{B(\alpha, \beta)} x^{\alpha - 1} {(1-x)}^{\beta-1}$$

其中，

$$\frac{1}{B(\alpha, \beta)} = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}$$

狄利克雷分布 Dirichlet Distribution

概率密度函数为：

$$f(x_1, x_2, ..., x_k; \alpha_1, \alpha_2, ..., \alpha_k) = \frac{1}{B(\alpha)} \prod_{i=1}^{k}{x_i}^{\alpha^i-1}$$

其中，

$$B(\alpha) = \frac{\prod_{i=1}^{k}\Gamma(\alpha^i)}{\Gamma(\sum_{i=1}^{k}\alpha^i)}, \sum_{i=1}^{k}x^i = 1$$

共轭分布 Conjugate Distribution

在贝叶斯理论中，如果后验概率分布 $P(\theta | x)$ 与先验概率分布 $P(\theta)$ 具有相同形式，则先验分布与后验分布被称为共轭分布，先验分布被称为似然函数的共轭先验。

$$P(\theta | x) = \frac{P(\theta, x)} {P(x)}$$

共轭先验的好处主要在于代数上的方便性，可以直接给出后验分布的封闭形式，否则的话只能数值计算。共轭先验也有助于获得关于似然函数如何更新先验分布的直观印象。

为什么要讲共轭分布呢？

联系到前文提到的贝叶斯理论，因为我们希望先验分布和似然对应的后验分布，在后面还可以作为先验分布！就像上面例子里的 “102个好人和101个的坏人” ，它既是前面一次贝叶斯推荐的后验分布，又是后一次贝叶斯推荐的先验分布。换句话说，我们希望先验分布和后验分布的形式是一样的，这样的分布叫共轭分布。

根据 二项分布、贝塔分布、多项式分布、狄利克雷分布的公式，数学上可以推导出：

贝塔分布是二项式分布的共轭先验分布，狄利克雷分布是多项式分布的共轭先验分布。

---

隐含狄利克雷分布主题模型 LDA Topic Model

使用场景 Use Cases

• 自动推测出文档集中讨论的主题
• 推测出的主题信息可以用于总结和组织文档，也可以用于降低特征 (featurization) 和维度 (dimensionality)
  • 文档 X 在讨论什么？-> 主题识别
  • 文档 X 和 文档 Y 的相似度是多少？-> 文本相似度计算
  • 如果我对主题 Z 感兴趣，那么哪篇文档最对我的胃口？ -> 推荐系统
• 其他使用场景
  • 情感分析 Sentiment analysis
  • 图片目标定位 Object localization for images
  • 音乐自动谐波分析 Automatic harmonic analysis for music
  • 生物信息学 Bioinformatics

假设 Assumptions

• Documents with similar topics will use similar groups of words
• Document definitions / modeling:
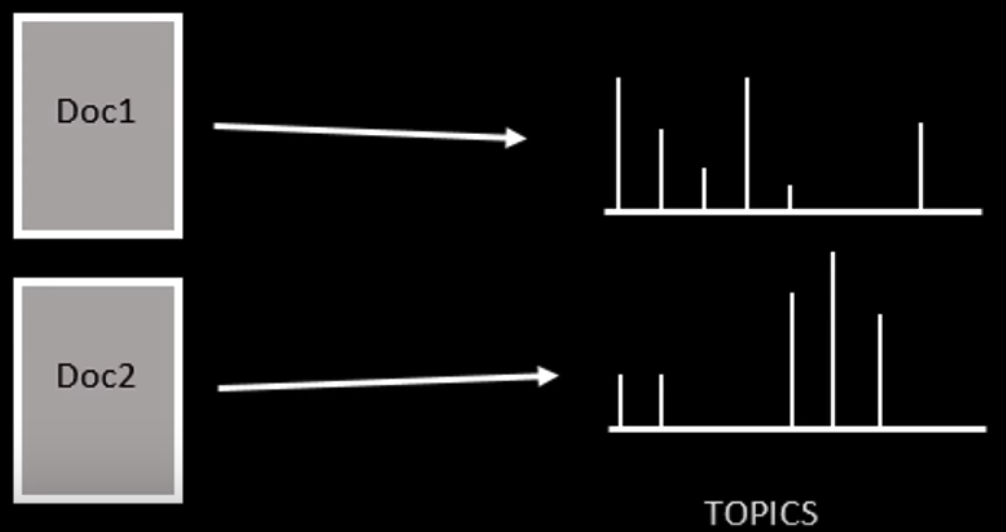
  • Documents are probability distributions over latent topics 文档是潜在主题的概率分布
  • Topics are probability distributions over words 主题是单词的概率分布

Doc - Topic Distribution

Topic - Word Distribution

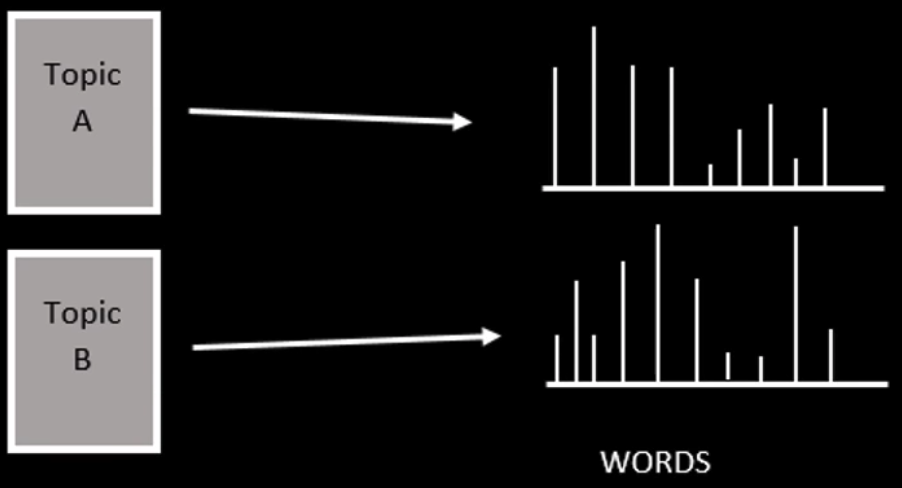
LDA 认为单词携带了强烈的语义信息，包含相似主题的文档中会出现相似的单词组。

一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成，每个主题都有一个单词的概率分布与之相关联。

LDA 模型与别的词袋模型的不同之处就在于，它利用了单词的概率分布而不是单词的出现频率。其他词袋模型可能会考虑文档中出现得最频繁的单词，而 LDA 使用了一种更全面的方法：考虑主题的单词分布。

盘子表示法 Plate Notation

当我们谈论 LDA 时，经常用盘子表示法来简洁地表达 LDA 模型参数间的依赖关系。

LDA 是一个三层贝叶斯模型，如下图所示，矩形框是“盘子”，代表复制品 (replicates)。

• 大盘子代表文档层
• 中盘子代表单词层
• 小盘子代表主题层

根据这些参数指向的位置 (落在哪个盘子中)，可以看出一个参数是应用于文档层，还是应用于主题层，还是单词层。

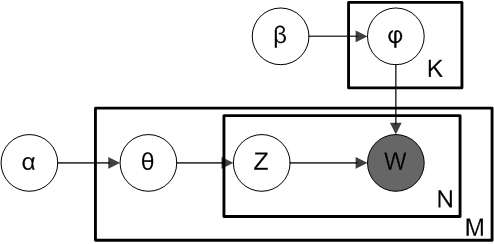
参数：

• $M$: 语料库中文档的数量
• $N$: 文档中单词的数量
• $K$: 语料库中主题的数量
• $\alpha$: 每篇文档的主题分布 (先验狄利克雷分布) 的参数，是一个 K 维向量，K 是主题数量
  • 越高，代表每篇文档可能包含更多的主题，而不只是包含一个或者两个特定的主题
  • 越低，代表每篇文档包含的主题数越少
• $\theta_i$: 文档 $i$ 的主题分布
• $z_{ij}$: 文档 $i$ 中第 $j$ 个单词的主题编号，服从多项式分布
• $\beta$: 每个主题的单词分布 (先验狄利克雷分布) 的参数，是一个 V 维向量，V 是文档中单词的数量
  • 越高，代表每个主题可能包含更多的单词
  • 越低，代表每个主题包含的单词数越少
• $\varphi{z{ij}}$: 主题 $z_{ij}$ 的单词分布
• $w_{ij}$: 特定的单词，服从多项式分布

生成过程 Generative Process

为了能比较好地理解 LDA 推测文档的主题分布的过程，先了解一篇文档的生成过程是很有帮助的。

LDA 认为一篇新文档是以这样的方式生成的：

• For each document $i$, draw $\theta_i \sim Dirichlet(\alpha), d = 1…D$
• For each word $j$ in document $i$:
  • Sample from $\thetai$ , draw a topic index $z{ij} \sim Multinomial(\theta_i)$
  • Sample from $\varphi{z{ij}}$ , draw the observed word $w{ij} \sim Multinomial(\varphi{z_{ij}})$

For parameter estimation, the posterior distribution is:

$$P(z, \theta, \varphi | w, \alpha, \beta) = \frac{P(z, \theta, \varphi | \alpha, \beta)}{P(w | \alpha, \beta)}$$

简单点，一篇文档的生成分为三步：

• 决定文档中单词的数量
• 给文档选择一个主题分布 (i.e. 20% topic A, 30% topic B, 50% topic C)
• 生成文档中的单词，通过：
  • 首先基于文档的主题分布选一个主题
  • 再基于主题的单词分布随机选一个单词
  • 重复上面两步，直到单词数量达到一开始设定的上限

举个栗子。

我们有一篇文章，它包含4个主题：Arts, Budgets, Children, Education。

如下图所示，每个主题可以被它下面的这些单词描述。

现在我们要写一篇包含这4个主题的文章

• 设定文档的长度为 1000 个词
• 假设文档的主题分布是：30% Arts, 20% Budgets, 30% Children, 20% Education
  • 首先基于文档的主题分布选一个主题 (根据我们的主题分布，1000 个词中大约 300 词来自主题 Arts)
  • 再基于主题的单词分布随机选一个单词
  • 重复上面两步 1000 次

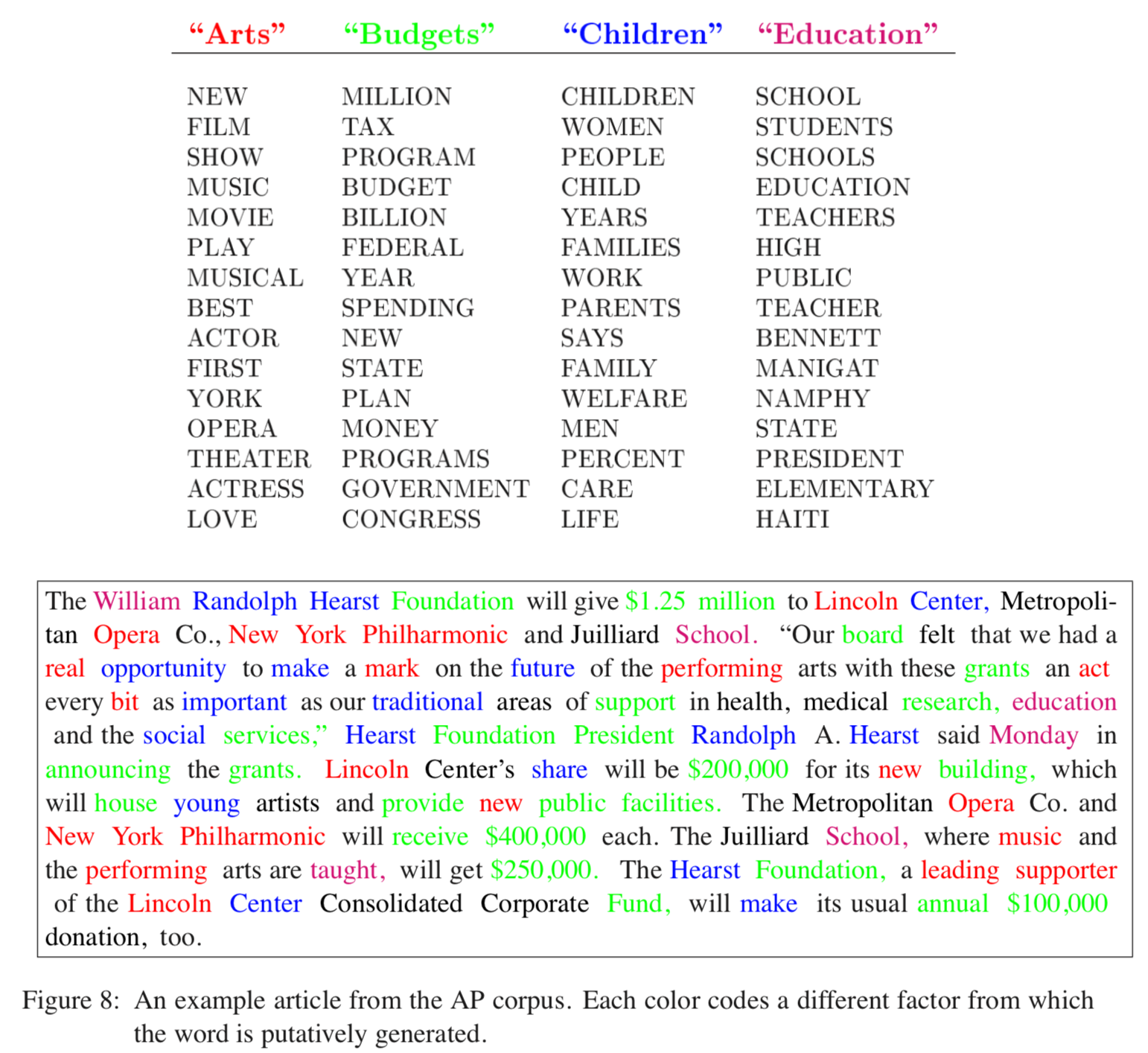
这就是 LDA 认为的人类写文章的过程。

在生成过程中文章的语法无关紧要，重要的是单词的分布，也许我们无法阅读生成后的文章，但是我们至少能知道这篇文章的主题是关于什么的。

值得注意的是，这个生成过程，从主题开始，不断挑选单词生成文档，它并不是 LDA 中运行的算法，而它的逆过程才是。

LDA 求解文档的主题分布实际上是上述生成过程的逆过程，从文档开始，反过来去发现文档中的主题。

• 生成过程：主题 -> 文档
• 逆过程：文档 -> 主题

如果只是想理解基本的 LDA 模型，到这里就可以了，如果想知道 LDA 模型的求解原理，让我们继续。

逆过程 Working Backwards

假如你有一个语料库 / 文档集，你希望 LDA 去学习每篇文档中 k 个主题的分布，以及每个主题的单词分布。

LDA 从文档层回溯，去推测哪些主题可能用于生成该文档。

• 随机给每篇文档中的每个单词分配 (assign) k 个主题中的一个主题
• 对于每篇文档 d，更新 (重新采样 Resample) 单词的主题
  • 假设除了当前文档之外的所有主题分配是正确的
  • 计算两个概率
    • 当前文档 d 中的单词被分配到主题 t 的概率 P(topic t | doc d)
    • 所有文档中被分配到主题 t 的单词中是单词 w 的概率 P(word w | topic t)
  • 基于这两个概率的乘积 P(topic t | doc d) * P(word w | topic t) 分配给单词 w 一个新的主题
• 不断重复上述步骤，最终达到稳定状态，这时可以认为所有主题的分配是合理的，得到文档的主题分布

根据上文提到的文档生成模型，两个概率的乘积 P(topic t | doc d) * P(word w | topic t) 就是主题 t 生成单词 w 的概率，所以用这个概率重新采样当前单词的主题是说得通的。

这个逆过程就是吉布斯采样。

解法 Existing Solutions

基于 LDA 模型如何求解 每一个主题的单词分布 和 每一篇文档的主题分布 呢？

有两种著名的算法，来估计 LDA 模型中的参数

• Variational EM (Expectation Maximization)
• Gibss Sampling

这两个算法都是批处理算法 (full batch algorithm)，运行时需要先把整个语料库读入内存，在每轮迭代中都会扫描 (scan) 语料库，这意味着巨大的内存压力。

当语料库很大的时候，批处理算法就显得力不从心了。如今，LDA 模型面对的输入语料库已经很大，比如 Wikipedia。

为了解决批处理算法带来的问题，Hoffman M, Bach F R, Blei D M 在 2010 年提出了 Online learning for LDA，该算法可以流式地处理大量的语料输入，并且在许多工业级的应用中都被证明有效。基本上现在主流的主题模型开源库中实现的 LDA 模型都是用的 Online LDA。

Online LDA Algorithm:

• is streamed: training documents may come in sequentially, no random access required.
• runs in constant memory w.r.t. the number of documents: size of the training corpus does not affect memory footprint, can process corpora larger than RAM, and
• is distributed: makes use of a cluster of machines, if available, to speed up model estimation.

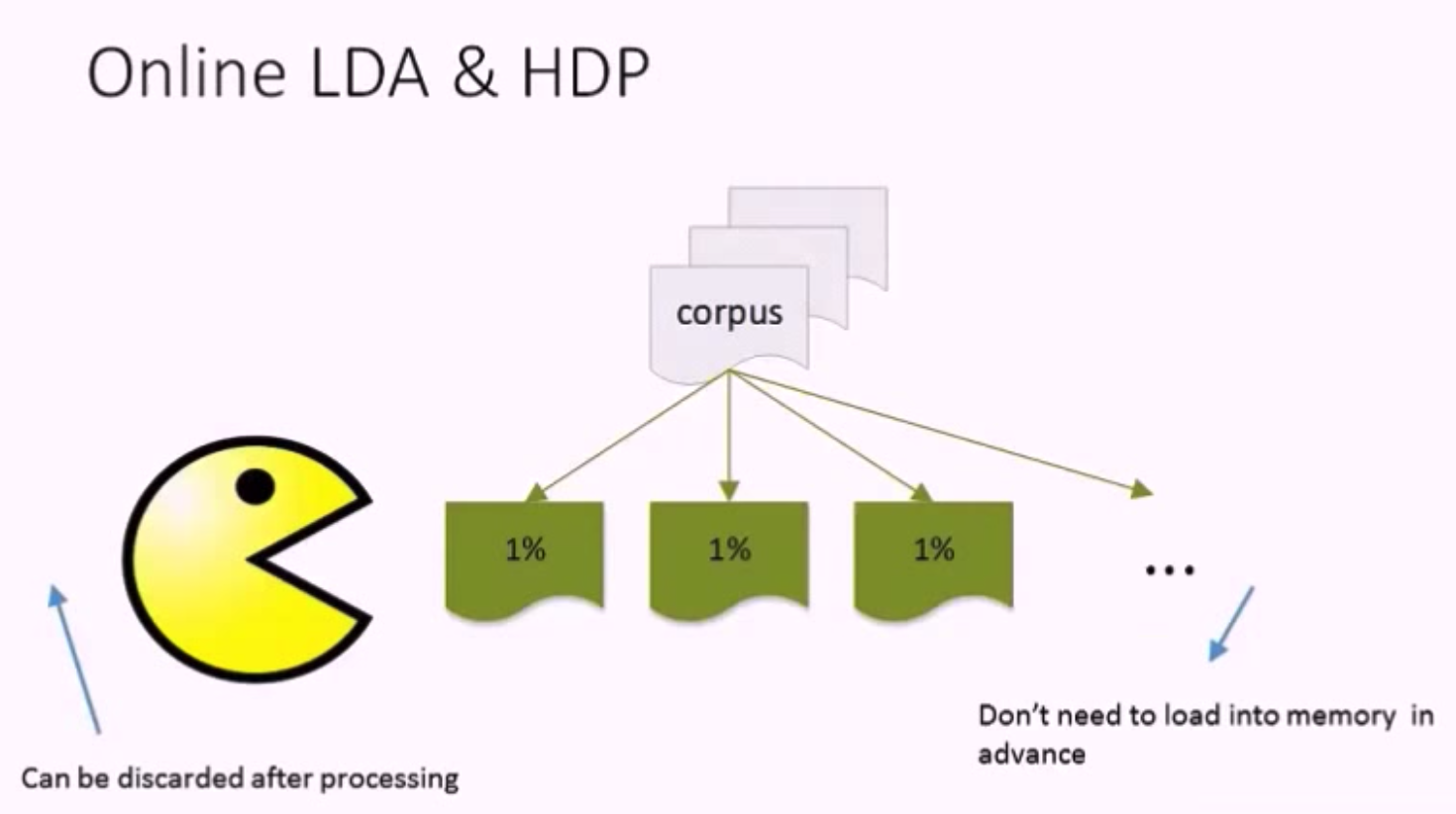
在 LDA 模型中，topic 的个数 K 的选取是一直都没有公认的好方法，原因在于不同任务对于推测主题的要求是存在差异的。

如果 LDA 是用于某个目标明确的学习任务 (比如分类)，那么就直接采用任务的指标来衡量就好了，能够实现分类效果最好的 topic 个数就是最合适的。

如果没有这样的任务怎么办？

业界最常用的指标包括 Perplexity，MPI-score 等，通过观察 Perplexity / MPI-score 这些指标随 topic 个数的变化曲线能够帮助我们选择合适的 topic 个数，比如可以找出曲线的拐点 (Perplexity 又小，topic 个数又少)。但是这些指标只能作为参考，而不能作为标准。

Yee Whye Teh 等人提出的层次狄利克雷过程 (Hierarchical Dirichlet Processes) 可以自动地确定 topic 的个数，也可以用于参考。

在现实中，肉眼看是一个简单有效的方法。

---

吉布斯采样算法 Gibss Sampling Algorithm

在 LDA 最初提出的时候，人们使用变分推断之 EM 算法进行求解，后来人们普遍开始使用较为简单的 Gibbs Sampling 来估计 LDA 参数，具体过程如下：

• 首先对所有文档中的所有词遍历一遍，为其都随机分配一个主题，即 $z_{m,n} = k \sim Mult(1/K)$ ,其中 $m$ 表示第 $m$ 篇文档，$n$ 表示文档中的第 $n$ 个词，$k$ 表示主题，$K$ 表示主题的总数，之后将对应的 $n^{(k)}_m+1, n_m+1, n^{(t)}_k+1, n_k+1$, 他们分别表示在 $m$ 文档中 $k$ 主题出现的次数，$m$ 文档中主题数量的和，$k$ 主题对应的 $t$ 词的次数，$k$ 主题对应的总词数。
• 之后对下述操作进行重复迭代。
• 对所有文档中的所有词进行遍历，假如当前文档 $m$ 的词 $t$ 对应主题为 $k$，则 $n^{(k)}_m-1, n_m-1, n^{(t)}_k-1, n_k-1$, 即先拿出当前词，之后根据 LDA 中 topic sample 的概率分布 sample 出新的主题，在对应的 $n^{(k)}_m, n_m, n^{(t)}_k, n_k$ 上分别 +1。

$$p(z_{i}=k|z_{-i},w) \propto \frac{(n_{k,-i}^{(t)} + \beta _{t})(n_{m,-i}^{(k)} + \alpha _{k})}{(\sum _{t=1}^{V}n_{k,-i}^{(t)} + \beta _{t})}$$

迭代完成后输出 主题-词矩阵 $\varphi$ 和 文档-主题矩阵 $\theta$

$$\phi _{k,t} = \frac{(n_{k}^{(t)} + \beta _{t})}{(n_{k} + \beta _{t})}$$ $$\theta _{m,k} = \frac{(n_{m}^{(k)} + \alpha _{k})}{(n_{m} + \alpha _{k})}$$

---

结论 Conclusions

文档是主题上的概率分布，主题是单词上的概率分布。

LDA 接受的输入是若干文档。她认为每篇文档中的单词是语义相关的。她试图想明白每篇文档是如何创造出来的。我们只需要告诉她有多少个主题需要构造，她就会根据主题的数量在语料库上生成主题和单词的分布。基于她的输出，可以预测新文档的主题分布，计算文档之间的相似度，文本分类。

LDA

• Input
  • 文档集 (Corpus)
  • K: the number of topics
• Output
  • 主题的单词分布 (Topic - Word Distribution) -> 每个主题在讨论什么
  • 文档的主题分布 (Doc - Topic Distribution) -> 每篇文档中包含了哪些主题

优点

• 对于每一个主题均可找出一些词语来描述它
• 是一个有效的主题建模工具
• 在许多领域已经展示出了很好的结果，比如推荐，文本分类

不足

• 必须事先指定主题的数量 K，而这个 K 的选取是困难的，需要大量的试验来确定
• 假如语料库中有许多关联的主题，狄利克雷主题分布无法捕捉主题间的相关性

---

References

• Blei, David M., Andrew Y. Ng, and Michael I. Jordan. “Latent dirichlet allocation.” Journal of machine Learning research3.Jan (2003): 993-1022.
• Hoffman, Blei, Bach: Online Learning for Latent Dirichlet Allocation, NIPS 2010.
• Hoffman M D, Blei D M, Wang C, et al. Stochastic variational inference[J]. The Journal of Machine Learning Research, 2013, 14(1): 1303-1347.
• LDA 数学八卦，rickjin
• 主题模型 LDA，邹博
• 通俗理解 LDA 主题模型，July
• 一文详解LDA主题模型，夏琦
• 文本主题模型之LDA，刘建平
• 隐含狄利克雷分布，维基百科
• 怎么确定LDA的topic个数？，知乎
• Topic modeling with Latent Dirichlet Allocation, Yuhao Yang
• LDA Topic Models, Andrius Knispellis
• Latent Dirichlet Allocation Algorithm Description, Scott Sullvan
• 徐亦达机器学习课程 Variational Inference Example - LDA, Yida Xu
• 周志华. 机器学习[M]. 清华大学出版社, 2016.
• Goodfellow I, Bengio Y, Courville A, et al. Deep learning[M]. Cambridge: MIT press, 2016. MLA
• 李航. “统计学习方法.” 清华大学出版社, 北京 (2012).

---

Open Source Libraries

• gensim LDA model
• sklearn LDA
• lda-project/lda
• baidu Familia