24 Puzzle Problem

Posted on | In | |

This article discusses about using A* Algorithm to solve 24 Puzzle Problem.

本文讲述了如何用A*算法解决24数码问题。

24 Puzzle

在5×5的棋盘，摆有24个棋子，每个棋子上标有1~24中的某一数字，不同棋子上标的数字不同。

棋盘上还有一个空白格，与空格相邻的棋子可以移到空白格中。反过来看，可以看成空白格移动到相邻的格子中。

24 Puzzle Problem: 给定一个初始状态和一个目标状态，从初始状态开始，通过空白格的移动，最后达到目标状态。

本文中，我们设置了2种目标状态，当然，你也可以根据自己的喜好来设置目标状态。

puzzle_sprial

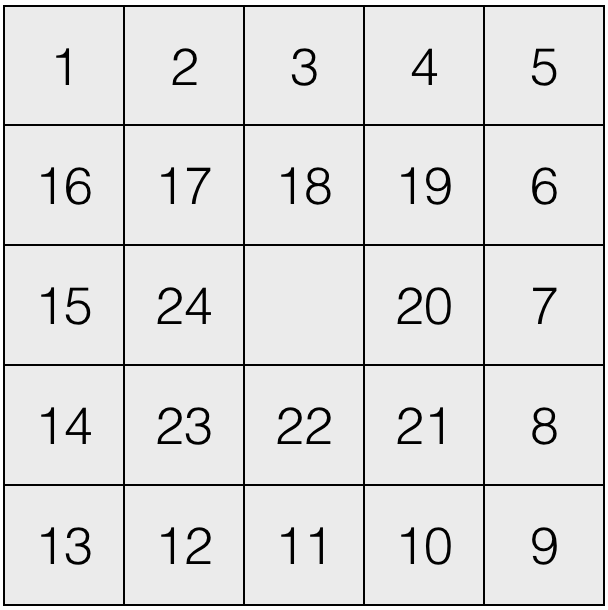
Fig. 1: Goal State 1 - SPRIAL

puzzle_normal

Fig. 2: Goal State 2 - NORMAL

有许多方法解决24数码问题，比如广度优先搜索法、A*、IDA*等。

一般来说，解24数码问题可以通过将棋盘的潜在状态存储成一棵树来解决。树中棋盘的每个状态都可以看做一个节点。

先看一个8数码问题的例子。

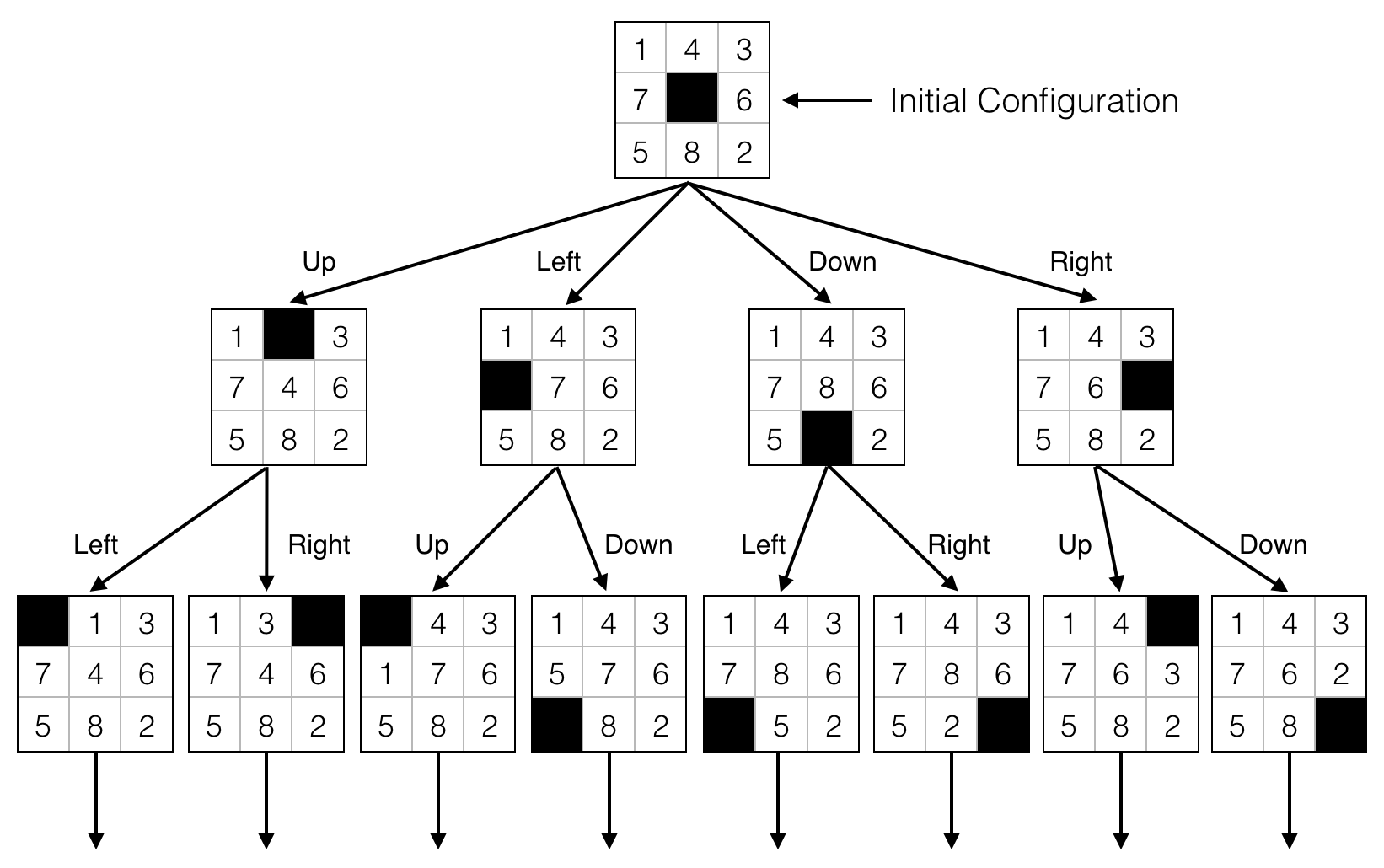
8puzzle

Fig. 3: The 8-Puzzle state space for a very simple example

广度优先搜索属于盲目搜索，往往是在搜索了大量无关的状态节点后才达到目标状态，甚至根本达不到目标状态。这就导致一颗巨大的树以至于耗尽内存，并且效率很低。

搜索是一种试探性的查寻过程，为了减少搜索的盲目性，增加试探的准确性，我们采用启发式搜索算法 (heuristic search)，本次实验中使用的是 A* 算法。

启发式搜索就是在搜索中要对每一个搜索的节点进行评估，从中选择最好、可能容易到达目标的节点，再从这个节点向前进行搜索，这样就可以在搜索中省略大量无关的节点，提高了效率。

A* Algorithm

这是一个启发式搜索算法，常用于寻找最短路径 (Pathfinding)。

一个节点的好坏用估价函数来对它进行评估。

A* 算法的估价函数可表示为： $F = G + H$

  • $G$ : 初始节点到当前节点的实际代价
  • $H$ : 对当前节点到目标节点的距离的启发式估计

每个节点都有自己的 $F$ 值，$G$ 值和 $H$ 值。$F$ 越小，节点越好。$H$ 的选择非常重要，对于不同的目标状态，应采取合理的启发式估计函数，

在搜索过程中，在扩展出一个节点后，要计算它的估价函数 F ，并对待拓展的节点排序，保证每次拓展的节点都是估价函数最小的。

数据结构：

  • openlist : 待拓展节点的队列，每次搜索都需要所有待拓展节点中 F 最小的那个节点。
  • closedlist : 已拓展节点的队列，每个节点存储有它的前驱节点的信息。

算法流程：

1
2
3
4
5
6
7
8
9
10
11
12
输入初始状态和目标状态；
判断问题是否有解(对奇数阶棋盘，只有当初始状态所有序列的逆序数为偶数时有解；对偶数阶棋盘，只有当初始状态所得序列的逆序数加其空格所在行数所得结果为偶数时有解)；
if(有解)
     将初始状态加入 openlist；
     while(未找到解 && openlist 非空)
     {
         从openlist中找出评价值 F 最小的节点，作为当前节点；
         判断当前节点状态和目标状态是否一致，若一致，break；否则下一步；
         检查当前节点周围的点，如果已经在openlist中看是否能通过当前点得到更小的 G，如果能就更新那个点的G, H 的值；如果在closedlist中或者是障碍物(不可达)则忽略它们; 如果可达且不在 openlist 中，将其加入 openlist；
         把当前节点从openlist中移除，加入closedlist中；
      }
保存路径，输出结果；

IDA* Algorithm

Iterative Deepening A*

  • 启发式搜索算法
  • 与 A* 相比，更高效，空间开销更小
  • 设置一个与初始状态的启发式估值相等的阈值 (threshold)
  • 实施深度优先搜索，当最新节点的估价超过阈值，则剪枝；假如搜索到解，返回它
  • 假如没有找到解，将阈值被超过的最小数值加到阈值上，重新开始搜索

Experiment

对于2种不同的目标状态，我们采用了2种不同启发式估计函数

  • 目标状态：普通 -> $H$: 当前节点与目标节点的曼哈顿距离
  • 目标状态：螺旋 -> $H$: Nilsson’s sequence score 尼尔森序列分数 $t = h + 3 × s$
    • 假如当前棋盘中心和目标状态的中心不匹配，$s$ 得1分
    • 假如当前方块顺时针方向上的第一个方块不是目标状态中它顺时针方向上第一个方块，那么 $s$ 得2分
    • $h$ 是当前节点与目标节点的曼哈顿距离

Gif 1: 24 Puzzle Solution - SPRIAL

Gif 2: 24 Puzzle Solution - NORMAL

感谢朴哥！

测试代码：24-puzzle

资磁一下？