Million Queens Problem

Posted on | In | |

This article discusses about how to solve Million Queens Problem in very short time.

本文介绍了一种在很短时间内解决百万皇后问题的算法。

N Queens Problem

国际象棋中，皇后可以在行、列和对角线行走。

假如在一个 N×N 的棋盘 (N=1 或 N>=4)，如何在棋盘上放置 N 个皇后，使得每个皇后处于安全的位置(不被其他皇后攻击)？

换句话说，使得每行、每列和每条对角线上不存在2个或2个以上的皇后。

这就是 N 皇后问题。

百万皇后问题即为 N 为百万数量级。

N 皇后问题是人工智能领域中一个经典的组合问题，在包括 VLSI (超大规模集成电路) 和交通控制等问题上有广泛应用。

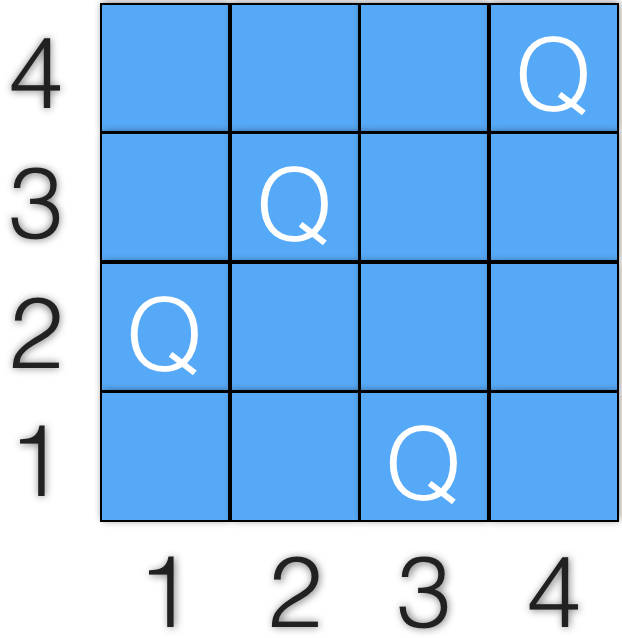
queen0

Fig. 1: an invalid solution for 4-queens

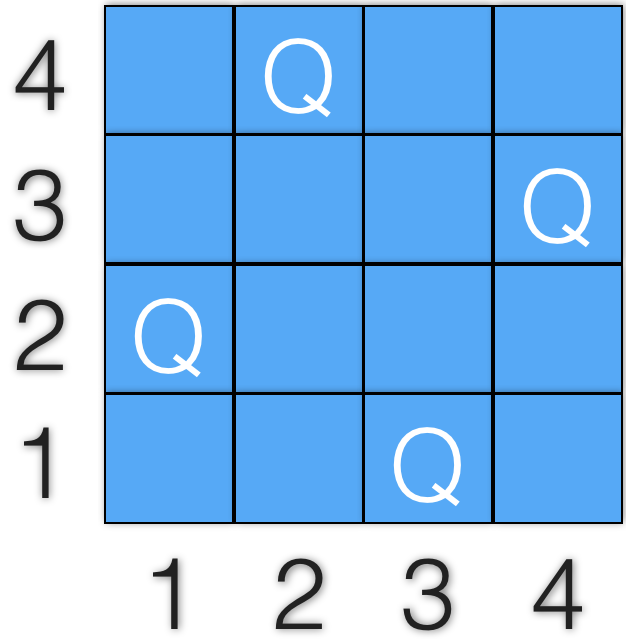
queen1

Fig. 2: a valid solution for 4-queens

Backtracking

N 皇后的经典求解方法是回溯法 (backtracking)，又称为试探法。

按照目标条件向前搜索，以达到目标。当探索到某一步，发现原先选择达不到目标，就退回一步重新搜索。这种走不通就退回再走的算法称为回溯法。

把 N 皇后的解表示成一个一维数组 a[N], 其中 a[i] 表示第 i 个皇后在第 i 行第 a[i] 列。

目标条件：

  • 所有皇后不能在同一行，a[i] 的定义就保证了这一点。
  • 所有皇后不能在同一列，因此 a[i] 数组中不能有相同的值。
  • 任意2个皇后不能在同一条对角线上，如何检测？2个皇后连成的直线斜率绝对值为1时它们在同一对角线上。

假设某一行为当前状态，不断检查该行所有的位置是否能放一个皇后，检索的状态有两种：

  • 先从首位开始检查，如果不能放置，接着检查该行第二个位置，依次检查下去，直到在该行找到一个可以放置一个皇后的地方，然后保存当前状态，转到下一行重复上述方法的检索。
  • 如果检查了该行所有的位置均不能放置一个皇后，说明上一行皇后放置的位置无法让所有的皇后找到自己合适的位置，因此就要回溯到上一行，重新检查该皇后位置后面的位置。

回溯法生成所有可能的 N 皇后的解。

Queen Search 1 Algorithm

解的结构：

每行一个解，用一个一维数组 queen[N] 保存解的列位置，queen[i] 表示第 i 个皇后在第 i 行第 queen[i] 列。数组queen是 1~N 的一个排列。

这样皇后不会在行或者列上冲突，我们只要解决对角线上的冲突问题。

Pseudocode:

1
2
3
4
5
6
7
8
9
// 产生一个随机的初始解的排列 queen
while(!collision)
{
     for all i, j in [0,N-1] && i!=j
     {
          if swap(queen[i], queen[j]) -> reduce collision
              do it
     }
}

同一条正对角线满足其行号与列号之差为常数，同一条负对角线满足其行号与列号之和为常数。

每一条对角线可以维护对应的冲突数，用数组 b 和 c 分别维护正对角线和负对角线的冲突数，数组长度都是 2N-1.

每次交换2个皇后会涉及8条对角线，因此 QS1 中判断交换能否减少冲突的时间是O(1)级别的。

N 皇后问题的最大冲突数为 N-1，for 循环运行的时间复杂度为 O(N^2) 且其成功运行至少减少1次冲突，所以 QS1 在一个随机解上的搜索的最坏时间复杂度为 O(N^3)。

Queen Search 4 Algorithm

QS1 中初始排列 queen 是完全随机的，这大概在对角线上会造成 0.53n 个冲突[1]。

假如让初始排列中的冲突数减少，会不会让 QS1 更高效呢？ 这就是 QS4 的背后的基本思想。

初始排列的生成:

  • 皇后是一行一行放置的
  • 新皇后的位置是在空闲列中随机生成的，直到找到一个无冲突的位置
  • 在放置了一定数量的无冲突的皇后之后，其他的皇后就在空闲列中完全随机生成了，不管对角线有没有冲突

皇后的无冲突数需要谨慎选择:

  • 如果太小，那么 QS4 相比 QS1 没什么提升
  • 如果太大，初始化时间太长

可能冲突的皇后数 c 与皇后数 n 相关。二者关系如下表。

皇后数 n 可能冲突数 c 无冲突数 m
n<=10 (n>8) ? 8 : n n-c
n<100 n 0
n<1000 30 n-30
n<10000 50 n-50
n<100000 80 n-80
n>=100000 100 n-100

Table 1: 可能冲突的皇后数 c 与皇后数 n 的关系

在初始排列生成后，至多 c 个皇后需要移动来寻找解。

QS4 中的搜索算法和 QS1 中类似：

  • 选择2个皇后，一个皇后来自可能冲突的皇后集合，另一个皇后完全随机选择。
  • 假如交换2个皇后的列位置可以减少冲突数，就交换；反之，不交换。
  • 搜索直到找到一个合法解结束。
  • 如果没有搜索到合法的解，那么就重新初始化。

QS4 算法将大部分时间花在了初始化上，搜索的过程耗时很短。

Thoughts

  • 解的结构是决定搜索性能的重要因素

  • 局部搜索可能会陷入局部搜索陷阱

    • 当一个随机解不能通过局部搜索消除所有冲突时，我们采用了随机重启的解决办法
    • N 皇后问题的可行解很多，所以可以通过随机解的局部搜索解决

References

  • [1] Sosic, R.; Gu, J. 3,000,000 Queens in less than one minute. ACM SIGART Bulletin, 1991, 2(2).
  • [2] Sosic, R.; Gu, J. A polynomial time algorithm for the N-Queens problem. ACM SIGART Bulletin, 1(3).
  • [3] Sosic, R.; Gu, J. Fast search algorithms for the n-queens problem. IEEE Transactions on Systems, Man and Cybernetics, 1991, 21(6): 1572 - 1576.
  • [4] Sosic, R.; Gu, J. Efficient local search with conflict minimization: a case study of the n-queens problem. IEEE Transactions on Knowledge and Data Engineering, 1994, 6(5):661 - 668

测试代码：million-queens

资磁一下？