Genetic Algorithm for Functional Maximum Problem

This article discusses about my personal understanding of using Genetic Algorithm to tackle Functional Maxmum Problem.

这篇文章讲述了我对于用遗传算法解决函数极值问题的一些见解。

大三的时候上了一门人工智能，其中有一次作业就用到了遗传算法，问题是这样的：

求解函数 f(x) = x + 10sin(5x) + 7cos(4x) 在区间[0,9]的最大值。

这个函数大概长这样：

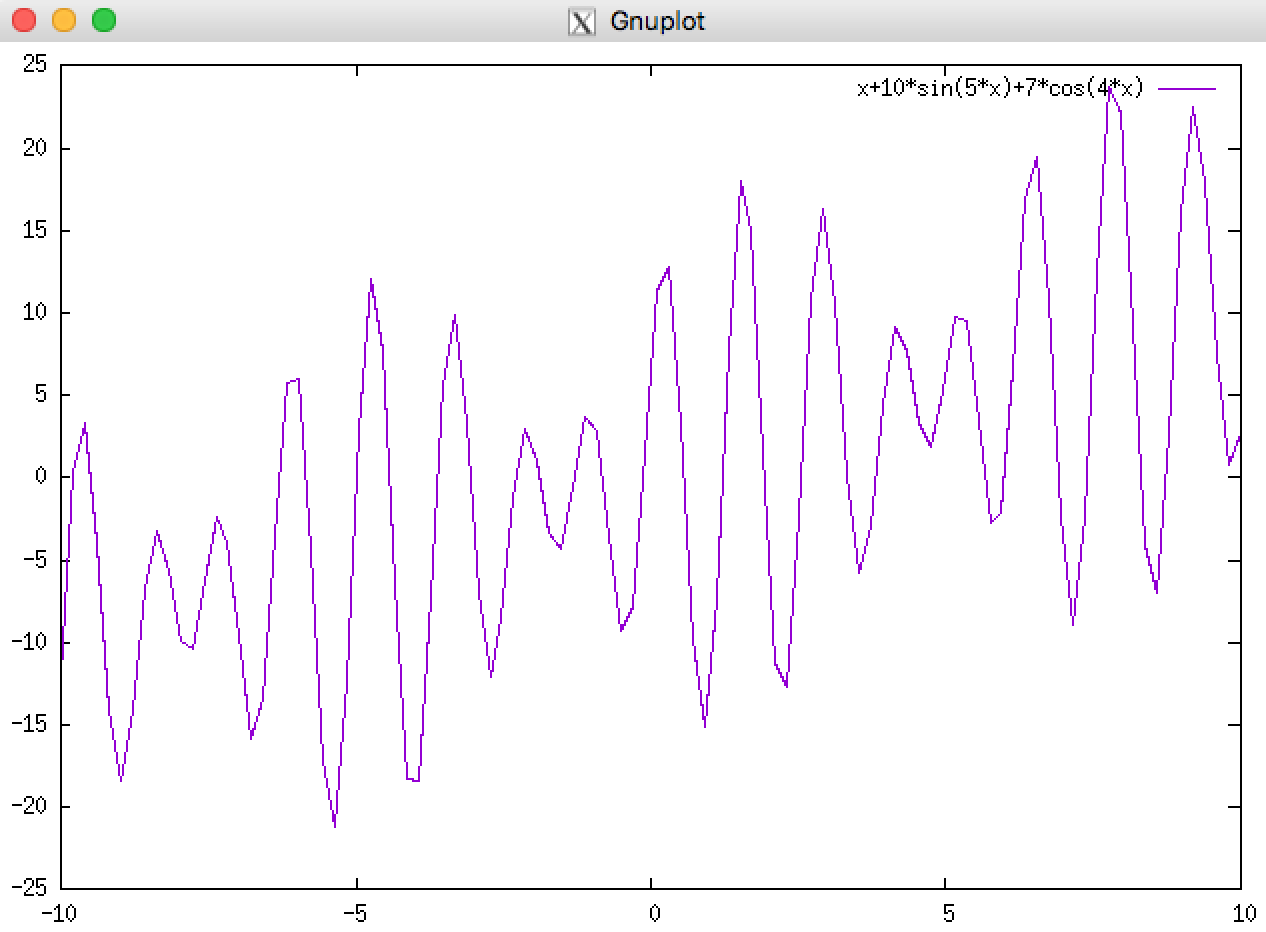
那么如何应用遗传算法如何来找到这个奇怪的函数的最大值呢？

事实上，不管一个函数的形状多么奇怪，遗传算法都能在很短的时间内找到它在一个区间内的(近似)最大值。

相当神奇，不是吗？

接下来围绕这个问题，讲讲我对遗传算法的一些理解。实现代码以及在Matlab中使用遗传算法的小教程都附在最后。

介绍 Introduction

遗传算法(Genetic Algorithm)遵循『适者生存』、『优胜劣汰』的原则，是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。

遗传算法模拟一个人工种群的进化过程，通过选择(Selection)、交叉(Crossover)以及变异(Mutation)等机制，在每次迭代中都保留一组候选个体，重复此过程，种群经过若干代进化后，理想情况下其适应度达到近似最优的状态。

自从遗传算法被提出以来，其得到了广泛的应用，特别是在函数优化、生产调度、模式识别、神经网络、自适应控制等领域，遗传算法发挥了很大的作用，提高了一些问题求解的效率。

遗传算法组成 GA Composition

编码 -> 创造染色体 Encode -> Chromosome
个体 -> 种群 Individual -> Population
适应度函数 Fitness Function
遗传算子 Genetic Operator
- 选择 Selection
- 交叉 Crossover
- 变异 Mutation
运行参数 Operation Parameter
- 是否选择精英操作 Elite Selection
- 种群大小 Population Size
- 染色体长度 Chromosome Length
- 最大迭代次数 Maximum Iterations
- 交叉概率 Crossover Rate
- 变异概率 Mutation Rate

编码与解码 Encode -> Chromosome

实现遗传算法的第一步就是明确对求解问题的编码和解码方式。

对于函数优化问题，一般有两种编码方式，各具优缺点

实数编码：直接用实数表示基因，容易理解且不需要解码过程，但容易过早收敛，从而陷入局部最优
二进制编码：稳定性高，种群多样性大，但需要的存储空间大，需要解码且难以理解

我选择的是二进制编码。

以我们的目标函数 $f(x)=x+10sin(5x)+7cos(4x), x\in{[0,9]}$ 为例。

假如设定求解的精度为小数点后4位，可以将x的解空间划分为 $(9-0)\times{10^{4}}=90000$ 个等分。

因为 $2^{16}<90000<2^{17}$ ，需要17位二进制数来表示这些解。

换句话说，一个解的编码就是一个17位的二进制串。

一开始，这些二进制串是随机生成的。

一个这样的二进制串代表一条染色体串，这里染色体串的长度为17。

对于任何一条这样的染色体chromosome，如何将它复原(解码)到 $[0,9]$ 这个区间中的数值呢？

对于本问题，我们可以采用以下公式来解码：
$x = 0+decimal(chromosome)\times{\frac{9-0}{2^{17}-1}}$

$decimal( )$: 将二进制数转化为十进制数

$chromosome$: 用二进制表示的一条染色体

一般化解码公式：
$f(x), x\in{[lowerbound, upperbound]}$
$x = lowerbound + decimal(chromosome)\times{\frac{upperbound-lowerbound}{2^{chromosomesize}-1}}$
$lowerbound$: 函数定义域的下限
$upperbound$: 函数定义域的上限
$chromosomesize$: 染色体的长度

通过上述公式，我们就可以成功地将二进制染色体串解码成 $[0,9]$ 区间中的十进制实数解。

个体与种群 Individual -> Population

『染色体』表达了某种特征，这种特征的载体，称为『个体』。

对于本次实验所要解决的一元函数最大值求解问题，个体可以用上一节构造的染色体表示，一个个体里有一条染色体。

许多这样的个体组成了一个种群，其含义是一个一维点集(x轴上 $[0,9]$ 的线段)。

适应度函数 Fitness Function

遗传算法中，一个个体(解)的好坏用适应度函数值来评价，在本问题中，$f(x)$ 就是适应度函数。

适应度函数值越大，解的质量越高。

适应度函数是遗传算法进化的驱动力，也是进行自然选择的唯一标准，它的设计应结合求解问题本身的要求而定。

遗传算子 Genetic Operator

我们希望有这样一个种群，它所包含的个体所对应的函数值都很接近于 $f(x)$ 在 $[0,9]$ 上的最大值，但是这个种群一开始可能不那么优秀，因为个体的染色体串是随机生成的。

如何让种群变得优秀呢？

不断的进化。

每一次进化都尽可能保留种群中的优秀个体，淘汰掉不理想的个体，并且在优秀个体之间进行染色体交叉，有些个体还可能出现变异。

种群的每一次进化，都会产生一个最优个体。种群所有世代的最优个体，可能就是函数 $f(x)$ 最大值对应的定义域中的点。

如果种群无休止地进化，那总能找到最好的解。但实际上，我们的时间有限，通常在得到一个看上去不错的解时，便终止了进化。

对于给定的种群，如何赋予它进化的能力呢？

首先是选择 (Selection)
- 选择操作是从前代种群中选择多对较优个体，一对较优个体称之为一对父母，让父母们将它们的基因传递到下一代，直到下一代个体数量达到种群数量上限
- 在选择操作前，将种群中个体按照适应度从小到大进行排列
- 采用轮盘赌选择方法（当然还有很多别的选择方法），各个个体被选中的概率与其适应度函数值大小成正比
- 轮盘赌选择方法具有随机性，在选择的过程中可能会丢掉较好的个体，所以可以使用精英机制，将前代最优个体直接选择
其次是交叉 (Crossover)
- 两个待交叉的不同的染色体(父母)根据交叉概率(cross_rate)按某种方式交换其部分基因
- 采用单点交叉法，也可以使用其他交叉方法
最后是变异 (Mutation)
- 染色体按照变异概率(mutate_rate)进行染色体的变异
- 采用单点变异法，也可以使用其他变异方法

一般来说，交叉概率(cross_rate)比较大，变异概率(mutate_rate)极低。

像求解函数最大值这类问题，我设置的交叉概率(cross_rate)是0.6，变异概率(mutate_rate)是0.01。

因为遗传算法相信2条优秀的父母染色体交叉更有可能产生优秀的后代，而变异的话产生优秀后代的可能性极低，不过也有存在可能一下就变异出非常优秀的后代。这也是符合自然界生物进化的特征的。

遗传算法流程 GA Flow

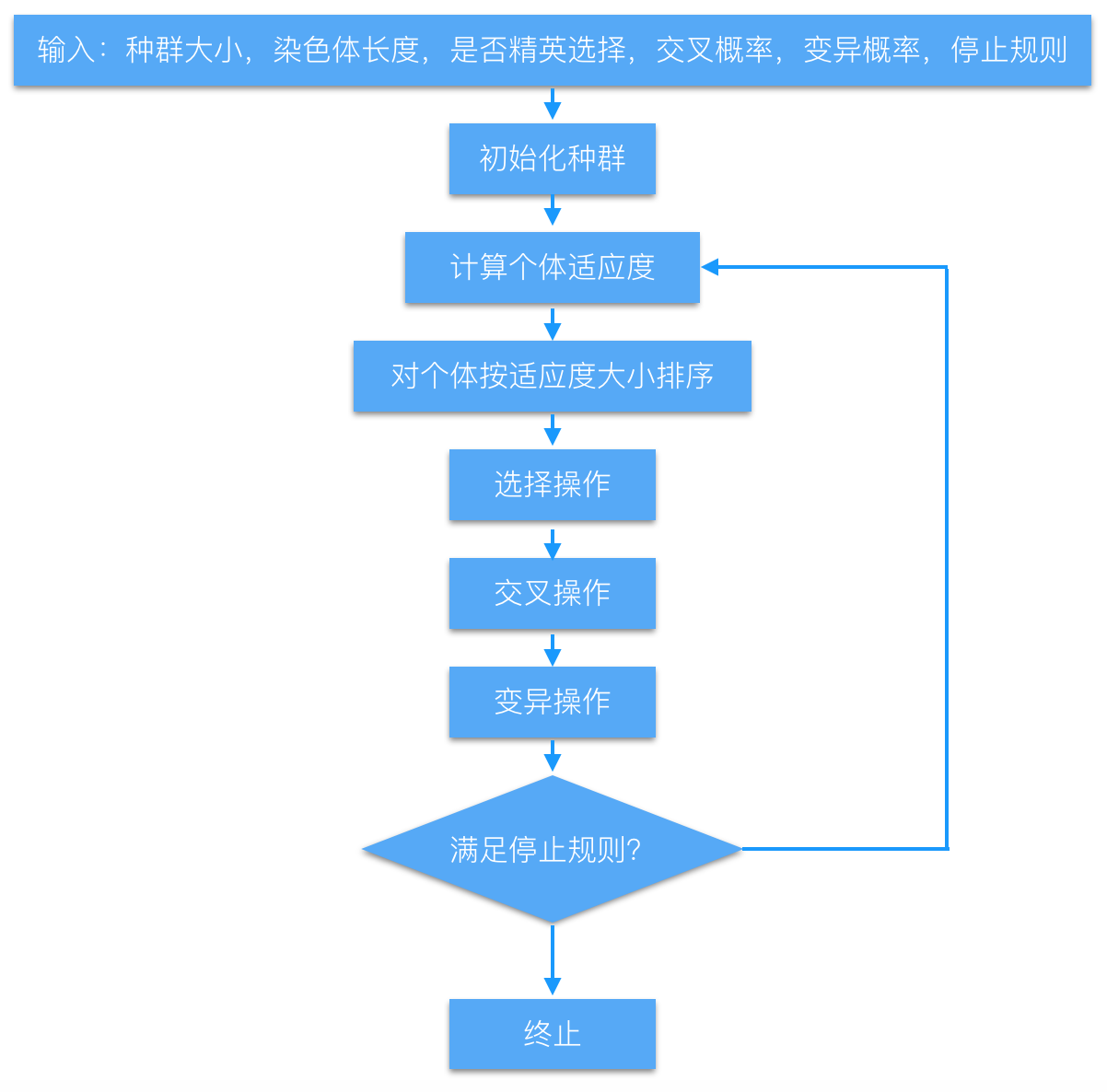
在matlab下写了个测试程序。

代码附在最后。

测试结果：

最优个体：00011111011111011
最优适应度：24.8554
最优个体对应自变量值：7.8569
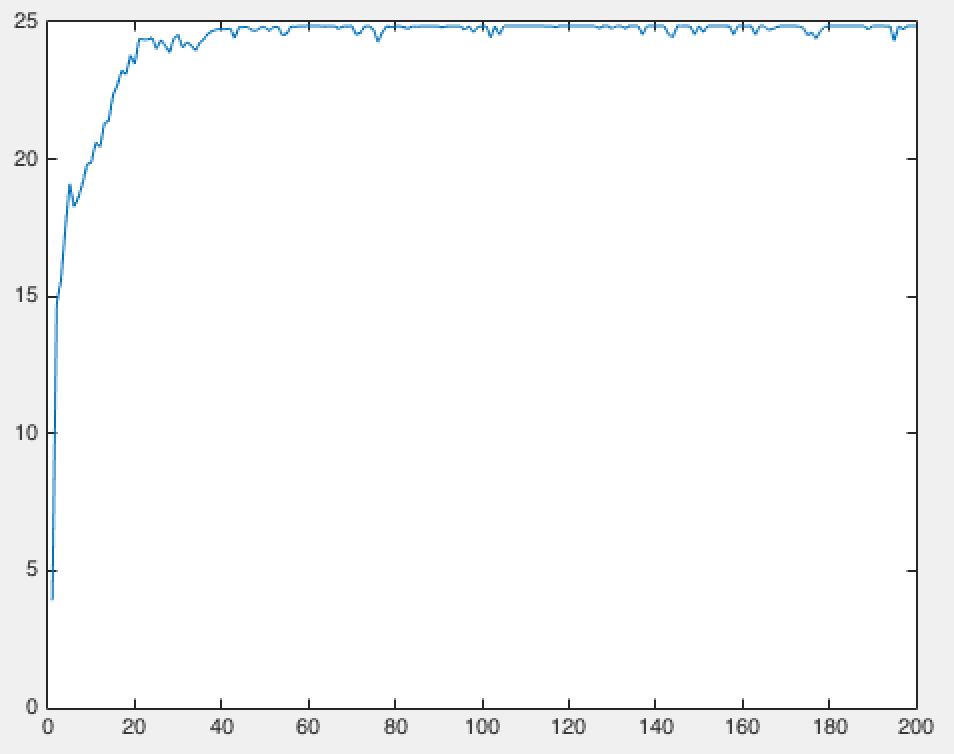
达到最优结果需要的迭代次数：多次实验后发现，达到收敛的迭代次数从20次到一百多次不等

迭代次数与平均适应度关系曲线（横轴：迭代次数，纵轴：平均适应度）

有现成的工具可以直接使用遗传算法，比如Matlab。
最后就再介绍一下如何在Matlab中使用遗传算法。

在MATLAB中使用GA

1.打开 Optimization 工具，在 Solver 中选择 ga - genetic algorithm，在 Fitness function 中填入 @target

2.在你的工程文件夹中新建 target.m，注意MATLAB的当前路径是你的工程文件夹所在路径

3.在 target.m 中写下适应度函数，比如

1
2
3

function [ y ] = target(x)
y = -x-10*sin(5*x)-7*cos(4*x);
end

注意：MATLAB中的GA只求解函数的(近似)最小值，所以先要将目标函数取反。

4.打开 Optimization 工具，输入变量个数(Number of variables) 和自变量定义域(Bounds)的值，点击 Start，遗传算法就跑起来了。最终在输出框中可以看到函数的(近似)最小值，和达到这一程度的迭代次数(Current iteration)和最终自变量的值(Final point)

5.在 Optimization - ga 工具中，有许多选项。通过这些选项，可以设置下列属性